LeetCode-in-Java

3625. Count Number of Trapezoids II

Hard

You are given a 2D integer array points where points[i] = [xi, yi] represents the coordinates of the ith point on the Cartesian plane.

Return the number of unique trapezoids that can be formed by choosing any four distinct points from points.

A trapezoid is a convex quadrilateral with at least one pair of parallel sides. Two lines are parallel if and only if they have the same slope.

Example 1:

Input: points = [[-3,2],[3,0],[2,3],[3,2],[2,-3]]

Output: 2

Explanation:

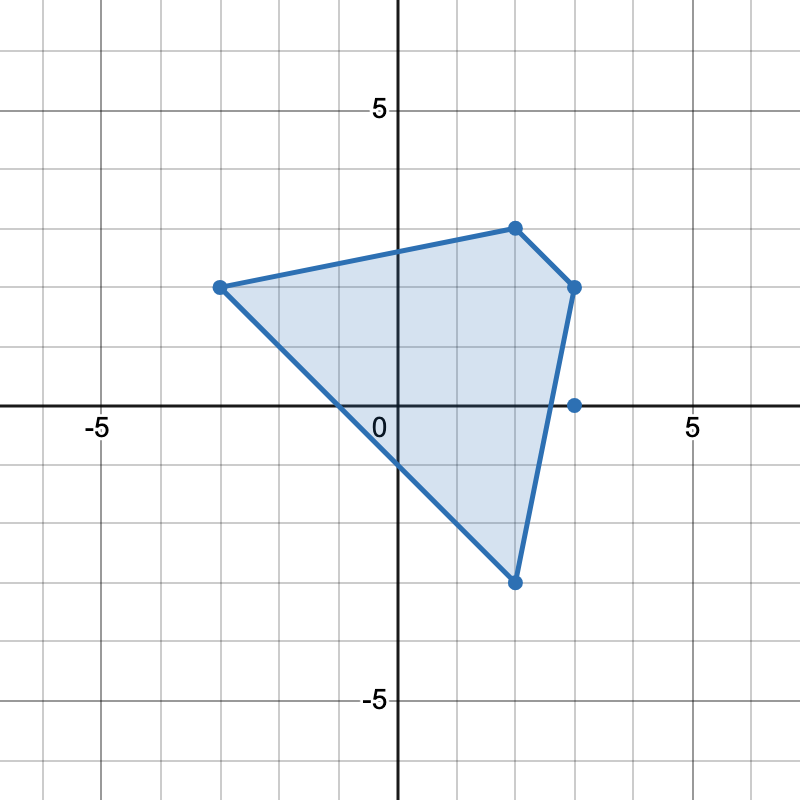
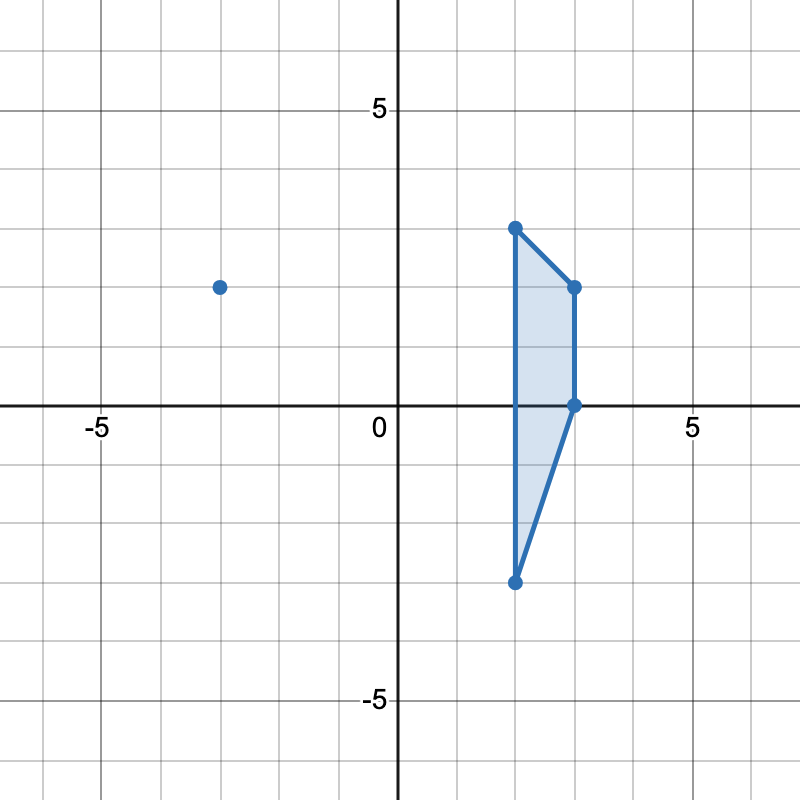
There are two distinct ways to pick four points that form a trapezoid:

• The points [-3,2], [2,3], [3,2], [2,-3] form one trapezoid.
• The points [2,3], [3,2], [3,0], [2,-3] form another trapezoid.

Example 2:

Input: points = [[0,0],[1,0],[0,1],[2,1]]

Output: 1

Explanation:

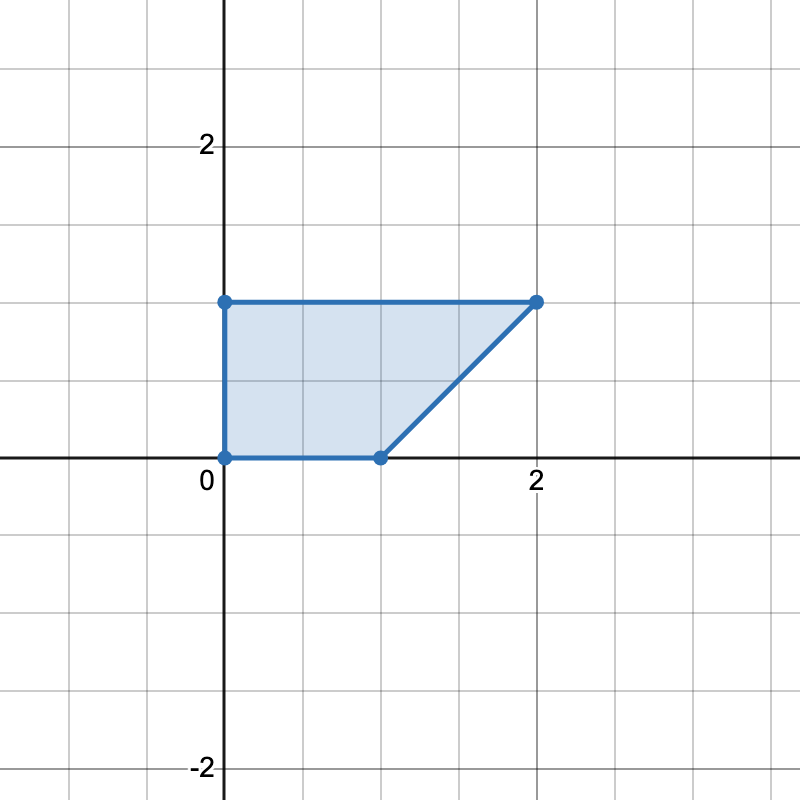
There is only one trapezoid which can be formed.

Constraints:

• 4 <= points.length <= 500
• –1000 <= xi, yi <= 1000
• All points are pairwise distinct.

Solution

import java.util.HashMap;
import java.util.Map;

public class Solution {
    private static class Slope {
        int dx;
        int dy;

        Slope(int dx, int dy) {
            this.dx = dx;
            this.dy = dy;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) {
                return true;
            }
            if (!(o instanceof Slope)) {
                return false;
            }
            Slope s = (Slope) o;
            return dx == s.dx && dy == s.dy;
        }

        @Override
        public int hashCode() {
            return dx * 1000003 ^ dy;
        }
    }

    private static class Pair {
        int a;
        int b;

        Pair(int a, int b) {
            this.a = a;
            this.b = b;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) {
                return true;
            }
            if (!(o instanceof Pair)) {
                return false;
            }
            Pair p = (Pair) o;
            return a == p.a && b == p.b;
        }

        @Override
        public int hashCode() {
            return a * 1000003 ^ b;
        }
    }

    public int countTrapezoids(int[][] points) {
        int n = points.length;
        Map<Slope, Map<Long, Integer>> slopeLines = new HashMap<>();
        Map<Pair, Map<Slope, Integer>> midpointSlopes = new HashMap<>();
        for (int i = 0; i < n; i++) {
            int x1 = points[i][0];
            int y1 = points[i][1];
            for (int j = i + 1; j < n; j++) {
                int x2 = points[j][0];
                int y2 = points[j][1];
                int dx = x2 - x1;
                int dy = y2 - y1;
                int g = gcd(Math.abs(dx), Math.abs(dy));
                dx /= g;
                dy /= g;
                if (dx < 0 || (dx == 0 && dy < 0)) {
                    dx = -dx;
                    dy = -dy;
                }
                int nx = -dy;
                int ny = dx;
                long lineId = (long) nx * x1 + (long) ny * y1;
                Slope slopeKey = new Slope(dx, dy);
                slopeLines
                        .computeIfAbsent(slopeKey, k -> new HashMap<>())
                        .merge(lineId, 1, Integer::sum);
                int mx = x1 + x2;
                int my = y1 + y2;
                Pair mid = new Pair(mx, my);
                midpointSlopes
                        .computeIfAbsent(mid, k -> new HashMap<>())
                        .merge(slopeKey, 1, Integer::sum);
            }
        }
        long trapezoidsRaw = 0;
        for (Map<Long, Integer> lines : slopeLines.values()) {
            if (lines.size() < 2) {
                continue;
            }
            long s = 0;
            long s2 = 0;
            for (Integer line : lines.values()) {
                s += line;
                s2 += (long) line * line;
            }
            trapezoidsRaw += (s * s - s2) / 2;
        }
        long parallelograms = 0;
        for (Map<Slope, Integer> mp : midpointSlopes.values()) {
            if (mp.size() < 2) {
                continue;
            }
            long s = 0;
            long s2 = 0;
            for (Integer num : mp.values()) {
                s += num;
                s2 += (long) num * num;
            }
            parallelograms += (s * s - s2) / 2;
        }
        long res = trapezoidsRaw - parallelograms;
        return res > Integer.MAX_VALUE ? Integer.MAX_VALUE : (int) res;
    }

    private int gcd(int a, int b) {
        while (b != 0) {
            int t = a % b;
            a = b;
            b = t;
        }
        return a == 0 ? 1 : a;
    }
}

This site is open source. Improve this page.