LeetCode-in-Java

3604. Minimum Time to Reach Destination in Directed Graph

Medium

You are given an integer n and a directed graph with n nodes labeled from 0 to n - 1. This is represented by a 2D array edges, where edges[i] = [ui, vi, starti, endi] indicates an edge from node ui to vi that can only be used at any integer time t such that starti <= t <= endi.

You start at node 0 at time 0.

In one unit of time, you can either:

• Wait at your current node without moving, or
• Travel along an outgoing edge from your current node if the current time t satisfies starti <= t <= endi.

Return the minimum time required to reach node n - 1. If it is impossible, return -1.

Example 1:

Input: n = 3, edges = [[0,1,0,1],[1,2,2,5]]

Output: 3

Explanation:

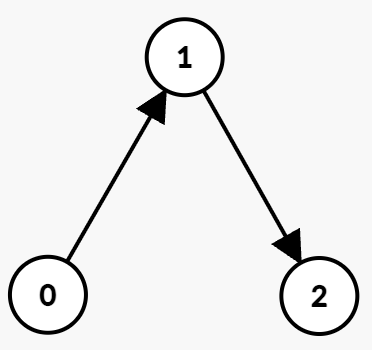
The optimal path is:

• At time t = 0, take the edge (0 → 1) which is available from 0 to 1. You arrive at node 1 at time t = 1, then wait until t = 2.
• At time t = `2`, take the edge (1 → 2) which is available from 2 to 5. You arrive at node 2 at time 3.

Hence, the minimum time to reach node 2 is 3.

Example 2:

Input: n = 4, edges = [[0,1,0,3],[1,3,7,8],[0,2,1,5],[2,3,4,7]]

Output: 5

Explanation:

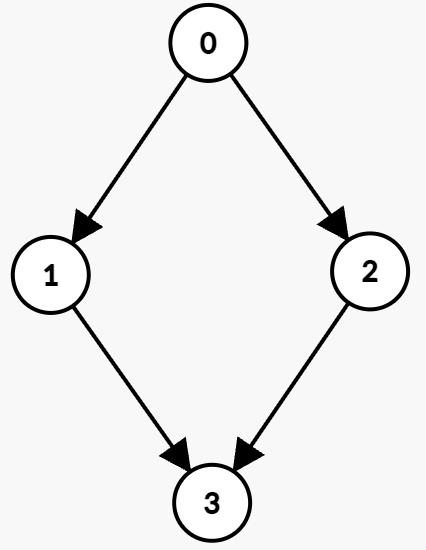
The optimal path is:

• Wait at node 0 until time t = 1, then take the edge (0 → 2) which is available from 1 to 5. You arrive at node 2 at t = 2.
• Wait at node 2 until time t = 4, then take the edge (2 → 3) which is available from 4 to 7. You arrive at node 3 at t = 5.

Hence, the minimum time to reach node 3 is 5.

Example 3:

Input: n = 3, edges = [[1,0,1,3],[1,2,3,5]]

Output: -1

Explanation:

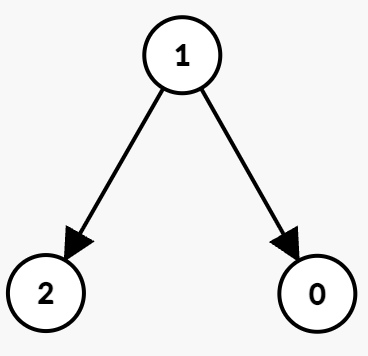
• Since there is no outgoing edge from node 0, it is impossible to reach node 2. Hence, the output is -1.

Constraints:

• 1 <= n <= 105
• 0 <= edges.length <= 105
• edges[i] == [ui, vi, starti, endi]
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= starti <= endi <= 109

Solution

import java.util.Arrays;

public class Solution {
    private static final int INF = Integer.MAX_VALUE;

    public int minTime(int n, int[][] edges) {
        int[] head = new int[n];
        int[] to = new int[edges.length];
        int[] start = new int[edges.length];
        int[] end = new int[edges.length];
        int[] next = new int[edges.length];
        Arrays.fill(head, -1);
        for (int i = 0; i < edges.length; i++) {
            int u = edges[i][0];
            to[i] = edges[i][1];
            start[i] = edges[i][2];
            end[i] = edges[i][3];
            next[i] = head[u];
            head[u] = i;
        }
        int[] heap = new int[n];
        int[] time = new int[n];
        int[] pos = new int[n];
        boolean[] visited = new boolean[n];
        int size = 0;
        for (int i = 0; i < n; i++) {
            time[i] = INF;
            pos[i] = -1;
        }
        time[0] = 0;
        heap[size] = 0;
        pos[0] = 0;
        size++;
        while (size > 0) {
            int u = heap[0];
            heap[0] = heap[--size];
            pos[heap[0]] = 0;
            heapifyDown(heap, time, pos, size, 0);
            if (visited[u]) {
                continue;
            }
            visited[u] = true;
            if (u == n - 1) {
                return time[u];
            }
            for (int e = head[u]; e != -1; e = next[e]) {
                int v = to[e];
                int t0 = time[u];
                if (t0 > end[e]) {
                    continue;
                }
                int arrival = Math.max(t0, start[e]) + 1;
                if (arrival < time[v]) {
                    time[v] = arrival;
                    if (pos[v] == -1) {
                        heap[size] = v;
                        pos[v] = size;
                        heapifyUp(heap, time, pos, size);
                        size++;
                    } else {
                        heapifyUp(heap, time, pos, pos[v]);
                    }
                }
            }
        }
        return -1;
    }

    private void heapifyUp(int[] heap, int[] time, int[] pos, int i) {
        while (i > 0) {
            int p = (i - 1) / 2;
            if (time[heap[p]] <= time[heap[i]]) {
                break;
            }
            swap(heap, pos, i, p);
            i = p;
        }
    }

    private void heapifyDown(int[] heap, int[] time, int[] pos, int size, int i) {
        while (2 * i + 1 < size) {
            int j = 2 * i + 1;
            if (j + 1 < size && time[heap[j + 1]] < time[heap[j]]) {
                j++;
            }
            if (time[heap[i]] <= time[heap[j]]) {
                break;
            }
            swap(heap, pos, i, j);
            i = j;
        }
    }

    private void swap(int[] heap, int[] pos, int i, int j) {
        int tmp = heap[i];
        heap[i] = heap[j];
        heap[j] = tmp;
        pos[heap[i]] = i;
        pos[heap[j]] = j;
    }
}

This site is open source. Improve this page.