LeetCode-in-Java

3558. Number of Ways to Assign Edge Weights I

Medium

There is an undirected tree with n nodes labeled from 1 to n, rooted at node 1. The tree is represented by a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates that there is an edge between nodes ui and vi.

Initially, all edges have a weight of 0. You must assign each edge a weight of either 1 or 2.

The cost of a path between any two nodes u and v is the total weight of all edges in the path connecting them.

Select any one node x at the maximum depth. Return the number of ways to assign edge weights in the path from node 1 to x such that its total cost is odd.

Since the answer may be large, return it modulo 109 + 7.

Note: Ignore all edges not in the path from node 1 to x.

Example 1:

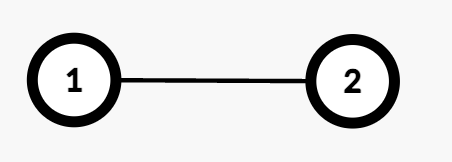
Input: edges = [[1,2]]

Output: 1

Explanation:

• The path from Node 1 to Node 2 consists of one edge (1 → 2).
• Assigning weight 1 makes the cost odd, while 2 makes it even. Thus, the number of valid assignments is 1.

Example 2:

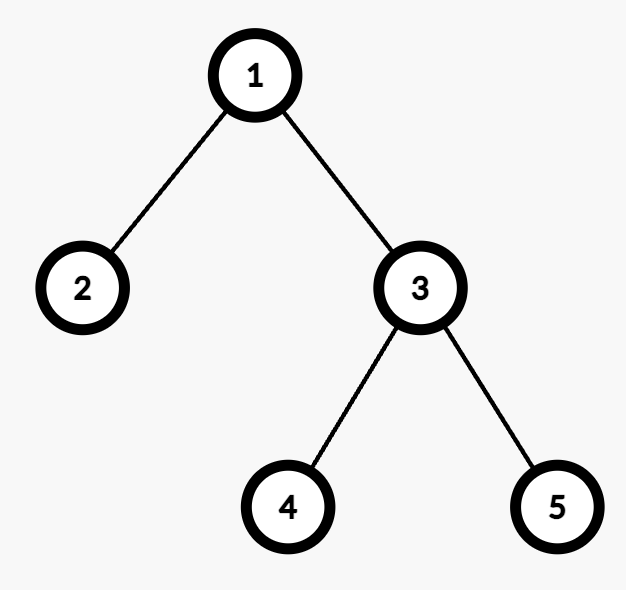
Input: edges = [[1,2],[1,3],[3,4],[3,5]]

Output: 2

Explanation:

• The maximum depth is 2, with nodes 4 and 5 at the same depth. Either node can be selected for processing.
• For example, the path from Node 1 to Node 4 consists of two edges (1 → 3 and 3 → 4).
• Assigning weights (1,2) or (2,1) results in an odd cost. Thus, the number of valid assignments is 2.

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i] == [ui, vi]
• 1 <= ui, vi <= n
• edges represents a valid tree.

Solution

public class Solution {
    private static final int MOD = (int) 1e9 + 7;
    private final long[] pow2 = new long[100001];

    public int assignEdgeWeights(int[][] edges) {
        if (pow2[0] == 0) {
            pow2[0] = 1;
            for (int i = 1; i < pow2.length; i++) {
                pow2[i] = (pow2[i - 1] << 1) % MOD;
            }
        }
        int n = edges.length + 1;
        int[] adj = new int[n + 1];
        int[] degrees = new int[n + 1];
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            adj[u] += v;
            adj[v] += u;
            degrees[u]++;
            degrees[v]++;
        }
        int[] que = new int[n];
        int write = 0;
        int read = 0;
        for (int i = 2; i <= n; ++i) {
            if (degrees[i] == 1) {
                que[write++] = i;
            }
        }
        int distance = 0;
        while (read < write) {
            distance++;
            int size = write - read;
            while (size-- > 0) {
                int v = que[read++];
                int u = adj[v];
                adj[u] -= v;
                if (--degrees[u] == 1 && u != 1) {
                    que[write++] = u;
                }
            }
        }
        return (int) pow2[distance - 1];
    }
}

This site is open source. Improve this page.