LeetCode-in-Java

3548. Equal Sum Grid Partition II

Hard

You are given an m x n matrix grid of positive integers. Your task is to determine if it is possible to make either one horizontal or one vertical cut on the grid such that:

• Each of the two resulting sections formed by the cut is non-empty.
• The sum of elements in both sections is equal, or can be made equal by discounting at most one single cell in total (from either section).
• If a cell is discounted, the rest of the section must remain connected.

Return true if such a partition exists; otherwise, return false.

Note: A section is connected if every cell in it can be reached from any other cell by moving up, down, left, or right through other cells in the section.

Example 1:

Input: grid = [[1,4],[2,3]]

Output: true

Explanation:

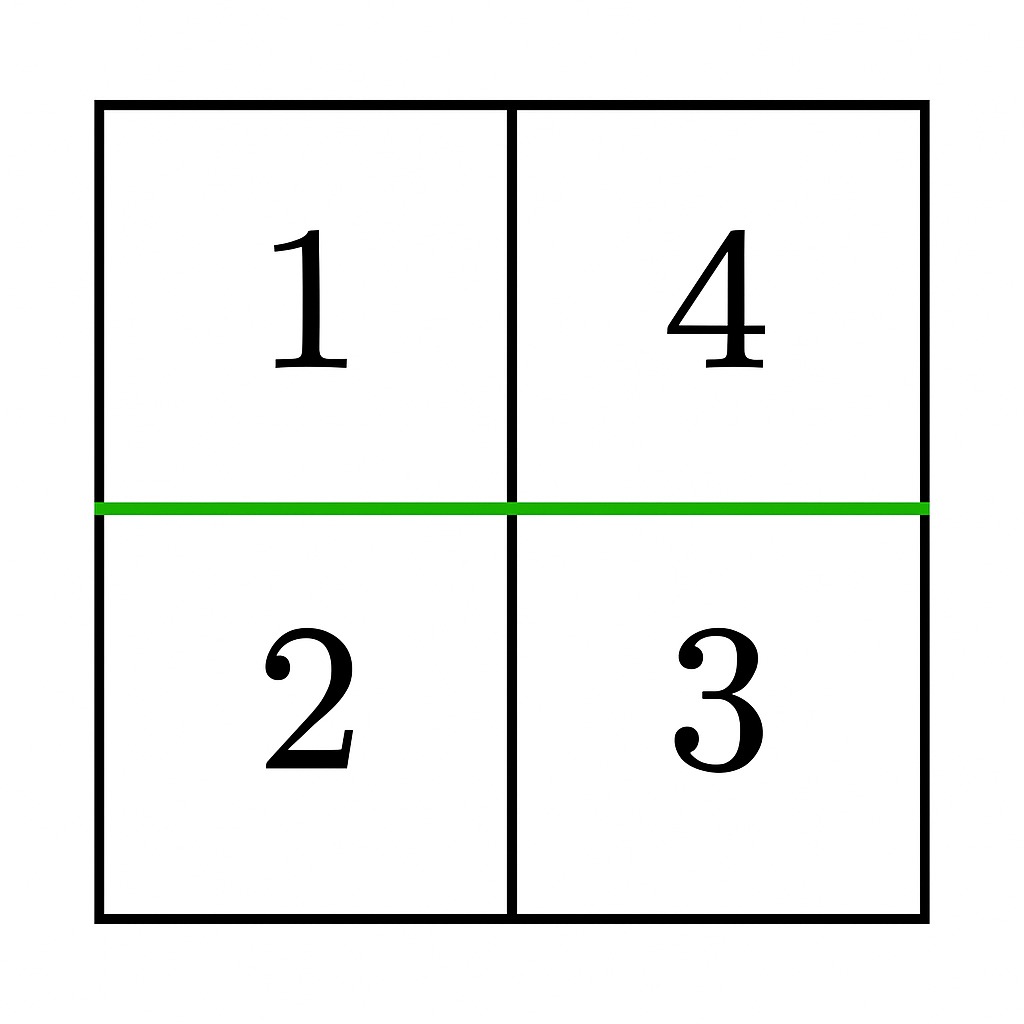
• A horizontal cut after the first row gives sums 1 + 4 = 5 and 2 + 3 = 5, which are equal. Thus, the answer is true.

Example 2:

Input: grid = [[1,2],[3,4]]

Output: true

Explanation:

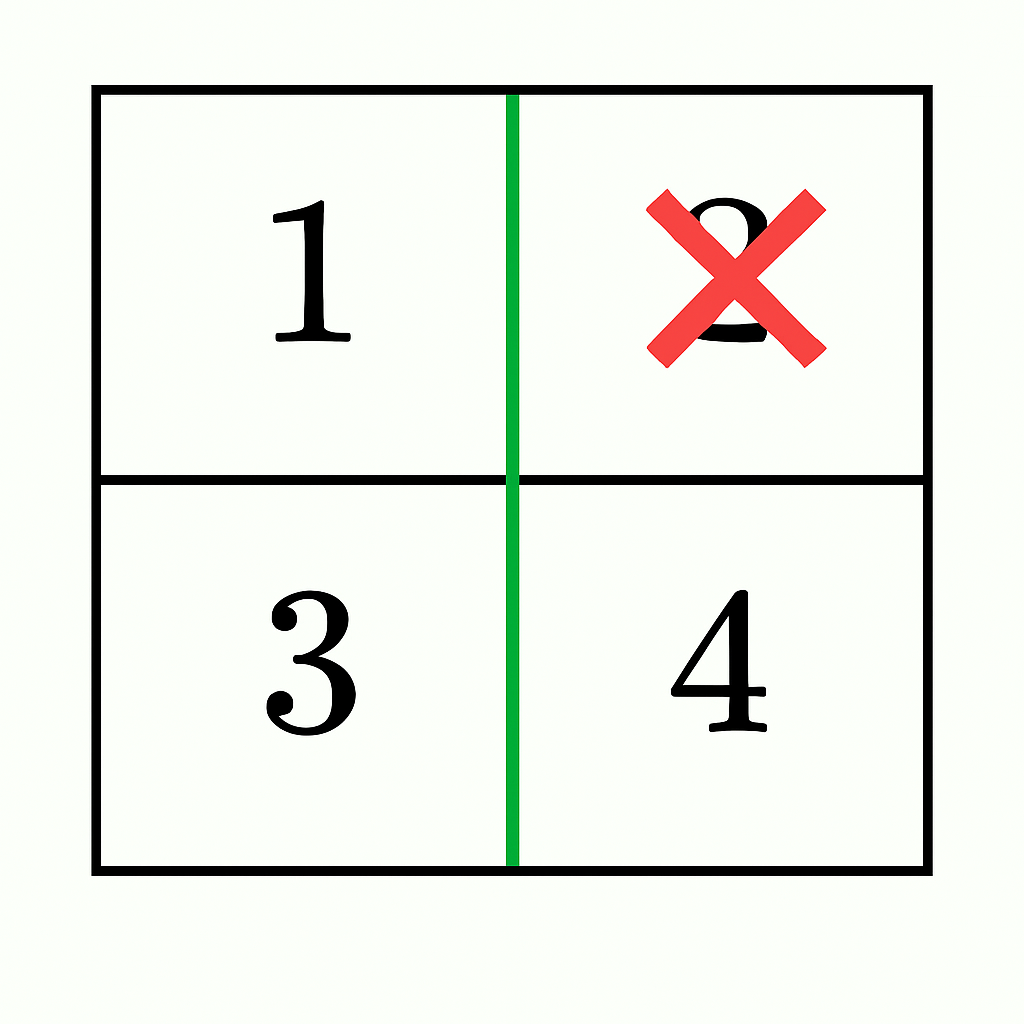
• A vertical cut after the first column gives sums 1 + 3 = 4 and 2 + 4 = 6.
• By discounting 2 from the right section (6 - 2 = 4), both sections have equal sums and remain connected. Thus, the answer is true.

Example 3:

Input: grid = [[1,2,4],[2,3,5]]

Output: false

Explanation:

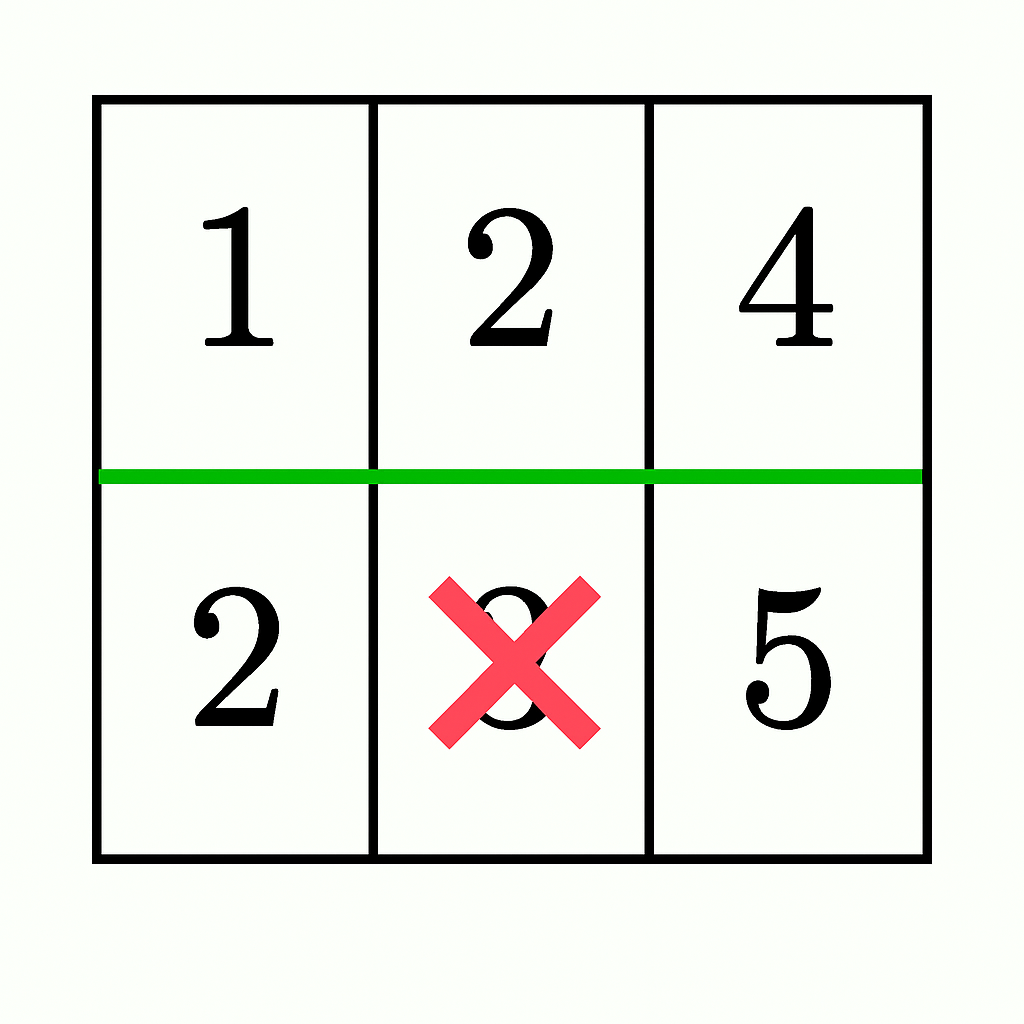
• A horizontal cut after the first row gives 1 + 2 + 4 = 7 and 2 + 3 + 5 = 10.
• By discounting 3 from the bottom section (10 - 3 = 7), both sections have equal sums, but they do not remain connected as it splits the bottom section into two parts ([2] and [5]). Thus, the answer is false.

Example 4:

Input: grid = [[4,1,8],[3,2,6]]

Output: false

Explanation:

No valid cut exists, so the answer is false.

Constraints:

• 1 <= m == grid.length <= 105
• 1 <= n == grid[i].length <= 105
• 2 <= m * n <= 105
• 1 <= grid[i][j] <= 105

Solution

public class Solution {
    private static final int MAX_SIZE = 100001;

    private long calculateSum(int[][] grid, int[] count) {
        long sum = 0;
        for (int[] line : grid) {
            for (int num : line) {
                sum += num;
                count[num]++;
            }
        }
        return sum;
    }

    private boolean checkHorizontalPartition(int[][] grid, long sum, int[] count) {
        int[] half = new int[MAX_SIZE];
        long now = 0;
        int m = grid.length;
        int n = grid[0].length;
        for (int i = 0; i < m - 1; i++) {
            for (int j = 0; j < n; j++) {
                now += grid[i][j];
                count[grid[i][j]]--;
                half[grid[i][j]]++;
            }
            if (now * 2 == sum) {
                return true;
            }
            if (now * 2 > sum) {
                long diff = now * 2 - sum;
                if (diff <= MAX_SIZE - 1 && half[(int) diff] > 0) {
                    if (n > 1) {
                        if (i > 0 || grid[0][0] == diff || grid[0][n - 1] == diff) {
                            return true;
                        }
                    } else {
                        if (i > 0 && (grid[0][0] == diff || grid[i][0] == diff)) {
                            return true;
                        }
                    }
                }
            } else {
                long diff = sum - now * 2;
                if (diff <= MAX_SIZE - 1 && count[(int) diff] > 0) {
                    if (n > 1) {
                        if (i < m - 2 || grid[m - 1][0] == diff || grid[m - 1][n - 1] == diff) {
                            return true;
                        }
                    } else {
                        if (i > 0 && (grid[m - 1][0] == diff || grid[i + 1][0] == diff)) {
                            return true;
                        }
                    }
                }
            }
        }
        return false;
    }

    private boolean checkVerticalPartition(int[][] grid, long sum) {
        int[] count = new int[MAX_SIZE];
        int[] half = new int[MAX_SIZE];
        for (int[] line : grid) {
            for (int num : line) {
                count[num]++;
            }
        }
        long now = 0;
        int m = grid.length;
        int n = grid[0].length;
        for (int i = 0; i < n - 1; i++) {
            for (int[] ints : grid) {
                now += ints[i];
                count[ints[i]]--;
                half[ints[i]]++;
            }
            if (now * 2 == sum) {
                return true;
            }
            if (now * 2 > sum) {
                long diff = now * 2 - sum;
                if (diff <= MAX_SIZE - 1 && half[(int) diff] > 0) {
                    if (m > 1) {
                        if (i > 0 || grid[0][0] == diff || grid[m - 1][0] == diff) {
                            return true;
                        }
                    } else {
                        if (i > 0 && (grid[0][0] == diff || grid[0][i] == diff)) {
                            return true;
                        }
                    }
                }
            } else {
                long diff = sum - now * 2;
                if (diff <= MAX_SIZE - 1 && count[(int) diff] > 0) {
                    if (m > 1) {
                        if (i < n - 2 || grid[0][n - 1] == diff || grid[m - 1][n - 1] == diff) {
                            return true;
                        }
                    } else {
                        if (i > 0 && (grid[0][n - 1] == diff || grid[0][i + 1] == diff)) {
                            return true;
                        }
                    }
                }
            }
        }
        return false;
    }

    public boolean canPartitionGrid(int[][] grid) {
        int[] count = new int[MAX_SIZE];
        long sum = calculateSum(grid, count);
        return checkHorizontalPartition(grid, sum, count) || checkVerticalPartition(grid, sum);
    }
}

This site is open source. Improve this page.