LeetCode-in-Java

3544. Subtree Inversion Sum

Hard

You are given an undirected tree rooted at node 0, with n nodes numbered from 0 to n - 1. The tree is represented by a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates an edge between nodes ui and vi.

You are also given an integer array nums of length n, where nums[i] represents the value at node i, and an integer k.

You may perform inversion operations on a subset of nodes subject to the following rules:

• Subtree Inversion Operation:

  • When you invert a node, every value in the subtree rooted at that node is multiplied by -1.

• Distance Constraint on Inversions:

  • You may only invert a node if it is “sufficiently far” from any other inverted node.

  • Specifically, if you invert two nodes a and b such that one is an ancestor of the other (i.e., if LCA(a, b) = a or LCA(a, b) = b), then the distance (the number of edges on the unique path between them) must be at least k.

Return the maximum possible sum of the tree’s node values after applying inversion operations.

Example 1:

Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], nums = [4,-8,-6,3,7,-2,5], k = 2

Output: 27

Explanation:

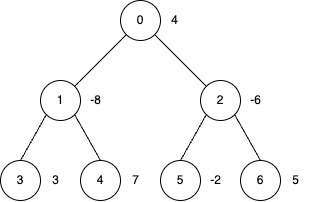
• Apply inversion operations at nodes 0, 3, 4 and 6.
• The final nums array is [-4, 8, 6, 3, 7, 2, 5], and the total sum is 27.

Example 2:

Input: edges = [[0,1],[1,2],[2,3],[3,4]], nums = [-1,3,-2,4,-5], k = 2

Output: 9

Explanation:

• Apply the inversion operation at node 4.
• The final nums array becomes [-1, 3, -2, 4, 5], and the total sum is 9.

Example 3:

Input: edges = [[0,1],[0,2]], nums = [0,-1,-2], k = 3

Output: 3

Explanation:

Apply inversion operations at nodes 1 and 2.

Constraints:

• 2 <= n <= 5 * 104
• edges.length == n - 1
• edges[i] = [ui, vi]
• 0 <= ui, vi < n
• nums.length == n
• -5 * 104 <= nums[i] <= 5 * 104
• 1 <= k <= 50
• The input is generated such that edges represents a valid tree.

Solution

import java.util.ArrayList;
import java.util.List;

public class Solution {
    private long[] totalSum;
    private int[] nums;
    private List<List<Integer>> nei;
    private int k;

    private long getTotalSum(int p, int cur) {
        long res = nums[cur];
        for (int c : nei.get(cur)) {
            if (c == p) {
                continue;
            }
            res += getTotalSum(cur, c);
        }
        totalSum[cur] = res;
        return res;
    }

    private void add(long[][] a, long[][] b) {
        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < a[0].length; j++) {
                a[i][j] += b[i][j];
            }
        }
    }

    private long[][] getMaxInc(int p, int cur) {
        long[][] ret = new long[3][k];
        for (int c : nei.get(cur)) {
            if (c == p) {
                continue;
            }
            add(ret, getMaxInc(cur, c));
        }
        long maxCandWithoutInv = nums[cur] + ret[2][0];
        long maxCandWithInv = -(totalSum[cur] - ret[0][k - 1]) - ret[1][k - 1];
        long minCandWithoutInv = nums[cur] + ret[1][0];
        long minCandWithInv = -(totalSum[cur] - ret[0][k - 1]) - ret[2][k - 1];
        long[][] res = new long[3][k];
        for (int i = 0; i < k - 1; i++) {
            res[0][i + 1] = ret[0][i];
            res[1][i + 1] = ret[1][i];
            res[2][i + 1] = ret[2][i];
        }
        res[0][0] = totalSum[cur];
        res[1][0] =
                Math.min(
                        Math.min(maxCandWithoutInv, maxCandWithInv),
                        Math.min(minCandWithoutInv, minCandWithInv));
        res[2][0] =
                Math.max(
                        Math.max(maxCandWithoutInv, maxCandWithInv),
                        Math.max(minCandWithoutInv, minCandWithInv));
        return res;
    }

    public long subtreeInversionSum(int[][] edges, int[] nums, int k) {
        totalSum = new long[nums.length];
        this.nums = nums;
        nei = new ArrayList<>();
        this.k = k;
        for (int i = 0; i < nums.length; i++) {
            nei.add(new ArrayList<>());
        }
        for (int[] e : edges) {
            nei.get(e[0]).add(e[1]);
            nei.get(e[1]).add(e[0]);
        }
        getTotalSum(-1, 0);
        long[][] res = getMaxInc(-1, 0);
        return res[2][0];
    }
}

This site is open source. Improve this page.