LeetCode-in-Java
3537. Fill a Special Grid
Medium
You are given a non-negative integer n representing a 2n x 2n grid. You must fill the grid with integers from 0 to 22n - 1 to make it special. A grid is special if it satisfies all the following conditions:
- All numbers in the top-right quadrant are smaller than those in the bottom-right quadrant.
- All numbers in the bottom-right quadrant are smaller than those in the bottom-left quadrant.
- All numbers in the bottom-left quadrant are smaller than those in the top-left quadrant.
- Each of its quadrants is also a special grid.
Return the special 2n x 2n grid.
Note: Any 1x1 grid is special.
Example 1:
Input: n = 0
Output: [[0]]
Explanation:
The only number that can be placed is 0, and there is only one possible position in the grid.
Example 2:
Input: n = 1
Output: [[3,0],[2,1]]
Explanation:
The numbers in each quadrant are:
- Top-right: 0
- Bottom-right: 1
- Bottom-left: 2
- Top-left: 3
Since 0 < 1 < 2 < 3, this satisfies the given constraints.
Example 3:
Input: n = 2
Output: [[15,12,3,0],[14,13,2,1],[11,8,7,4],[10,9,6,5]]
Explanation:
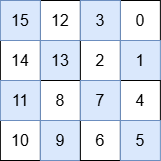
The numbers in each quadrant are:
- Top-right: 3, 0, 2, 1
- Bottom-right: 7, 4, 6, 5
- Bottom-left: 11, 8, 10, 9
- Top-left: 15, 12, 14, 13
max(3, 0, 2, 1) < min(7, 4, 6, 5)max(7, 4, 6, 5) < min(11, 8, 10, 9)max(11, 8, 10, 9) < min(15, 12, 14, 13)
This satisfies the first three requirements. Additionally, each quadrant is also a special grid. Thus, this is a special grid.
Constraints:
0 <= n <= 10
Solution
public class Solution {
public int[][] specialGrid(int n) {
if (n == 0) {
return new int[][] { {0}};
}
int len = (int) Math.pow(2, n);
int[][] ans = new int[len][len];
int[] num = new int[] {(int) Math.pow(2, 2D * n) - 1};
backtrack(ans, len, len, 0, 0, num);
return ans;
}
private void backtrack(int[][] ans, int m, int n, int x, int y, int[] num) {
if (m == 2 && n == 2) {
ans[x][y] = num[0];
ans[x + 1][y] = num[0] - 1;
ans[x + 1][y + 1] = num[0] - 2;
ans[x][y + 1] = num[0] - 3;
num[0] -= 4;
return;
}
backtrack(ans, m / 2, n / 2, x, y, num);
backtrack(ans, m / 2, n / 2, x + m / 2, y, num);
backtrack(ans, m / 2, n / 2, x + m / 2, y + n / 2, num);
backtrack(ans, m / 2, n / 2, x, y + n / 2, num);
}
}

