LeetCode-in-Java
3534. Path Existence Queries in a Graph II
Hard
You are given an integer n representing the number of nodes in a graph, labeled from 0 to n - 1.
You are also given an integer array nums of length n and an integer maxDiff.
An undirected edge exists between nodes i and j if the absolute difference between nums[i] and nums[j] is at most maxDiff (i.e., |nums[i] - nums[j]| <= maxDiff).
You are also given a 2D integer array queries. For each queries[i] = [ui, vi], find the minimum distance between nodes ui and vi. If no path exists between the two nodes, return -1 for that query.
Return an array answer, where answer[i] is the result of the ith query.
Note: The edges between the nodes are unweighted.
Example 1:
Input: n = 5, nums = [1,8,3,4,2], maxDiff = 3, queries = [[0,3],[2,4]]
Output: [1,1]
Explanation:
The resulting graph is:
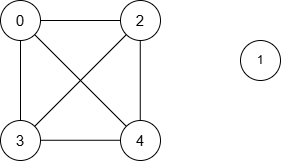
| Query | Shortest Path | Minimum Distance |
|---|---|---|
| [0, 3] | 0 → 3 | 1 |
| [2, 4] | 2 → 4 | 1 |
Thus, the output is [1, 1].
Example 2:
Input: n = 5, nums = [5,3,1,9,10], maxDiff = 2, queries = [[0,1],[0,2],[2,3],[4,3]]
Output: [1,2,-1,1]
Explanation:
The resulting graph is:
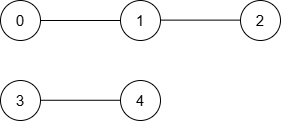
Here is the equivalent Markdown for the given HTML table:
| Query | Shortest Path | Minimum Distance |
|---|---|---|
| [0, 1] | 0 → 1 | 1 |
| [0, 2] | 0 → 1 → 2 | 2 |
| [2, 3] | None | -1 |
| [4, 3] | 3 → 4 | 1 |
Thus, the output is [1, 2, -1, 1].
Example 3:
Input: n = 3, nums = [3,6,1], maxDiff = 1, queries = [[0,0],[0,1],[1,2]]
Output: [0,-1,-1]
Explanation:
There are no edges between any two nodes because:
- Nodes 0 and 1:
|nums[0] - nums[1]| = |3 - 6| = 3 > 1 - Nodes 0 and 2:
|nums[0] - nums[2]| = |3 - 1| = 2 > 1 - Nodes 1 and 2:
|nums[1] - nums[2]| = |6 - 1| = 5 > 1
Thus, no node can reach any other node, and the output is [0, -1, -1].
Constraints:
1 <= n == nums.length <= 1050 <= nums[i] <= 1050 <= maxDiff <= 1051 <= queries.length <= 105queries[i] == [ui, vi]0 <= ui, vi < n
Solution
import java.util.Arrays;
@SuppressWarnings({"java:S135", "java:S6541"})
public class Solution {
public int[] pathExistenceQueries(int n, int[] nums, int maxDiff, int[][] queries) {
int[] position = new int[n];
int[] values = new int[n];
Integer[] sortedIndices = new Integer[n];
for (int i = 0; i < n; i++) {
sortedIndices[i] = i;
}
Arrays.sort(sortedIndices, (a, b) -> Integer.compare(nums[a], nums[b]));
for (int i = 0; i < n; i++) {
position[sortedIndices[i]] = i;
values[i] = nums[sortedIndices[i]];
}
int[] reachableIndex = new int[n];
int j = 0;
for (int i = 0; i < n; i++) {
if (j < i) {
j = i;
}
while (j + 1 < n && values[j + 1] - values[i] <= maxDiff) {
j++;
}
reachableIndex[i] = j;
}
int maxLog = 1;
while ((1 << maxLog) < n) {
maxLog++;
}
int[][] upTable = new int[maxLog][n];
upTable[0] = reachableIndex.clone();
for (int k = 1; k < maxLog; k++) {
for (int i = 0; i < n; i++) {
upTable[k][i] = upTable[k - 1][upTable[k - 1][i]];
}
}
int[] results = new int[queries.length];
for (int idx = 0; idx < queries.length; idx++) {
int start = queries[idx][0];
int end = queries[idx][1];
if (start == end) {
results[idx] = 0;
continue;
}
int startPos = position[start];
int endPos = position[end];
if (startPos > endPos) {
int temp = startPos;
startPos = endPos;
endPos = temp;
}
if (Math.abs(nums[start] - nums[end]) <= maxDiff) {
results[idx] = 1;
continue;
}
if (reachableIndex[startPos] < endPos) {
int current = startPos;
int jumpCount = 0;
for (int k = maxLog - 1; k >= 0; k--) {
if (upTable[k][current] < endPos) {
if (upTable[k][current] == current) {
break;
}
current = upTable[k][current];
jumpCount += 1 << k;
}
}
if (reachableIndex[current] >= endPos) {
results[idx] = jumpCount + 1;
} else {
results[idx] = -1;
}
} else {
results[idx] = 1;
}
}
return results;
}
}

