LeetCode-in-Java

3425. Longest Special Path

Hard

You are given an undirected tree rooted at node 0 with n nodes numbered from 0 to n - 1, represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, lengthi] indicates an edge between nodes ui and vi with length lengthi. You are also given an integer array nums, where nums[i] represents the value at node i.

A special path is defined as a downward path from an ancestor node to a descendant node such that all the values of the nodes in that path are unique.

Note that a path may start and end at the same node.

Return an array result of size 2, where result[0] is the length of the longest special path, and result[1] is the minimum number of nodes in all possible longest special paths.

Example 1:

Input: edges = [[0,1,2],[1,2,3],[1,3,5],[1,4,4],[2,5,6]], nums = [2,1,2,1,3,1]

Output: [6,2]

Explanation:

In the image below, nodes are colored by their corresponding values in nums

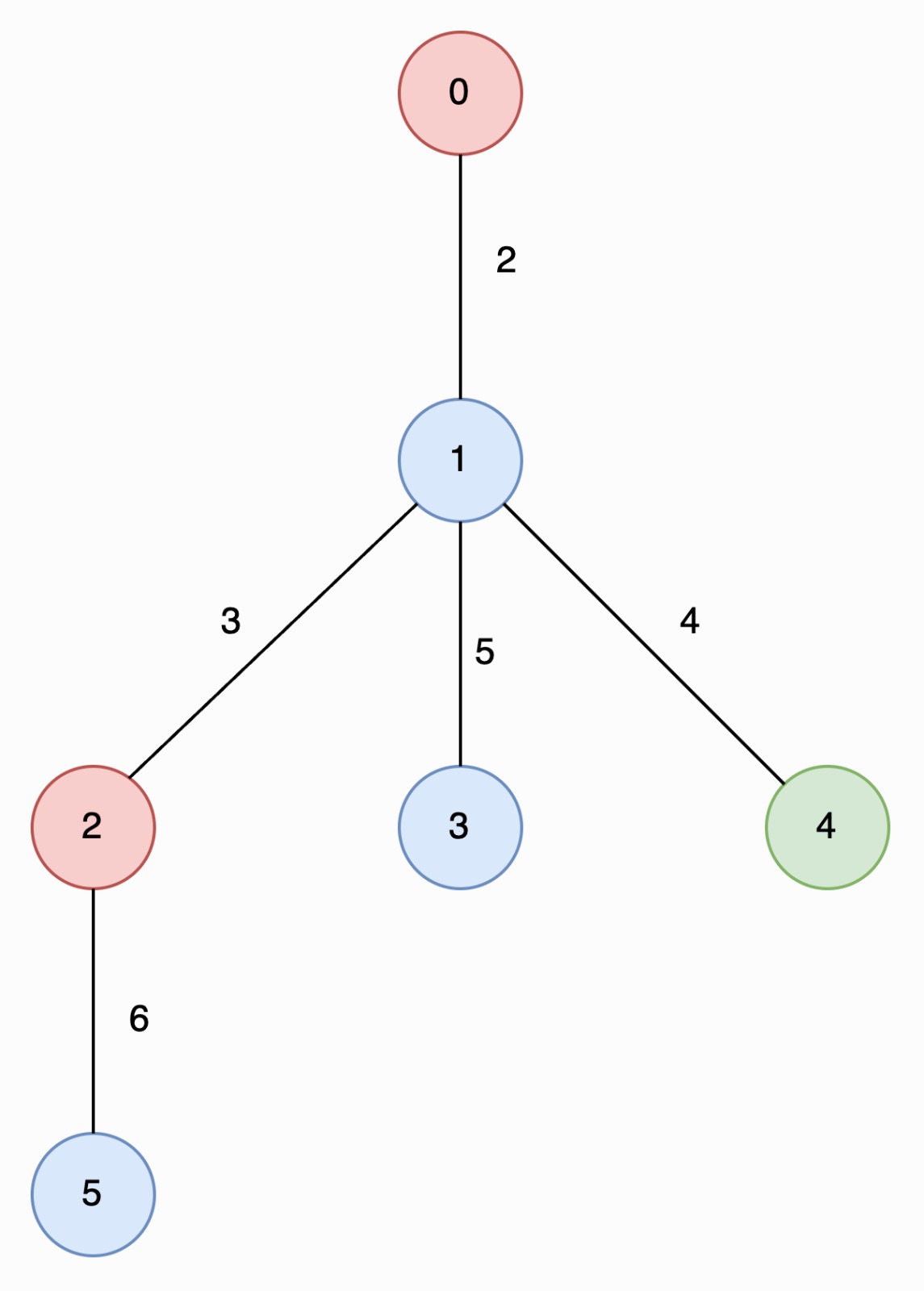
The longest special paths are 2 -> 5 and 0 -> 1 -> 4, both having a length of 6. The minimum number of nodes across all longest special paths is 2.

Example 2:

Input: edges = [[1,0,8]], nums = [2,2]

Output: [0,1]

Explanation:

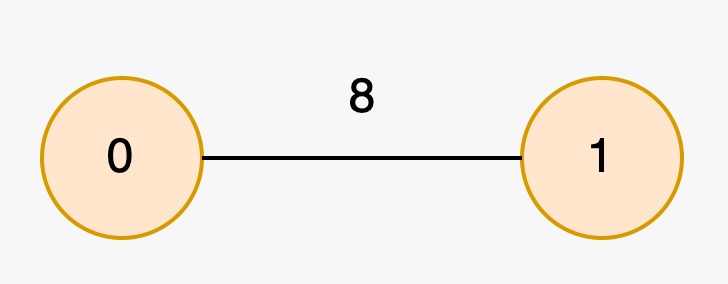
The longest special paths are 0 and 1, both having a length of 0. The minimum number of nodes across all longest special paths is 1.

Constraints:

• 2 <= n <= 5 * 104
• edges.length == n - 1
• edges[i].length == 3
• 0 <= ui, vi < n
• 1 <= lengthi <= 103
• nums.length == n
• 0 <= nums[i] <= 5 * 104
• The input is generated such that edges represents a valid tree.

Solution

import java.util.ArrayList;
import java.util.List;

@SuppressWarnings({"java:S107", "unchecked"})
public class Solution {
    public int[] longestSpecialPath(int[][] edges, int[] nums) {
        int n = edges.length + 1;
        int max = 0;
        List<int[]>[] adj = new List[n];
        for (int i = 0; i < n; i++) {
            adj[i] = new ArrayList<>();
            max = Math.max(nums[i], max);
        }
        for (int[] e : edges) {
            adj[e[0]].add(new int[] {e[1], e[2]});
            adj[e[1]].add(new int[] {e[0], e[2]});
        }
        int[] dist = new int[n];
        int[] res = new int[] {0, Integer.MAX_VALUE};
        int[] st = new int[n + 1];
        Integer[] seen = new Integer[max + 1];
        dfs(adj, nums, res, dist, seen, st, 0, -1, 0, 0);
        return res;
    }

    private void dfs(
            List<int[]>[] adj,
            int[] nums,
            int[] res,
            int[] dist,
            Integer[] seen,
            int[] st,
            int node,
            int parent,
            int start,
            int pos) {
        Integer last = seen[nums[node]];
        if (last != null && last >= start) {
            start = last + 1;
        }
        seen[nums[node]] = pos;
        st[pos] = node;
        int len = dist[node] - dist[st[start]];
        int sz = pos - start + 1;
        if (res[0] < len || res[0] == len && res[1] > sz) {
            res[0] = len;
            res[1] = sz;
        }
        for (int[] neighbor : adj[node]) {
            if (neighbor[0] == parent) {
                continue;
            }
            dist[neighbor[0]] = dist[node] + neighbor[1];
            dfs(adj, nums, res, dist, seen, st, neighbor[0], node, start, pos + 1);
        }
        seen[nums[node]] = last;
    }
}

This site is open source. Improve this page.