LeetCode-in-Java
3402. Minimum Operations to Make Columns Strictly Increasing
Easy
You are given a m x n matrix grid consisting of non-negative integers.
In one operation, you can increment the value of any grid[i][j] by 1.
Return the minimum number of operations needed to make all columns of grid strictly increasing.
Example 1:
Input: grid = [[3,2],[1,3],[3,4],[0,1]]
Output: 15
Explanation:
- To make the
0thcolumn strictly increasing, we can apply 3 operations ongrid[1][0], 2 operations ongrid[2][0], and 6 operations ongrid[3][0]. - To make the
1stcolumn strictly increasing, we can apply 4 operations ongrid[3][1].

Example 2:
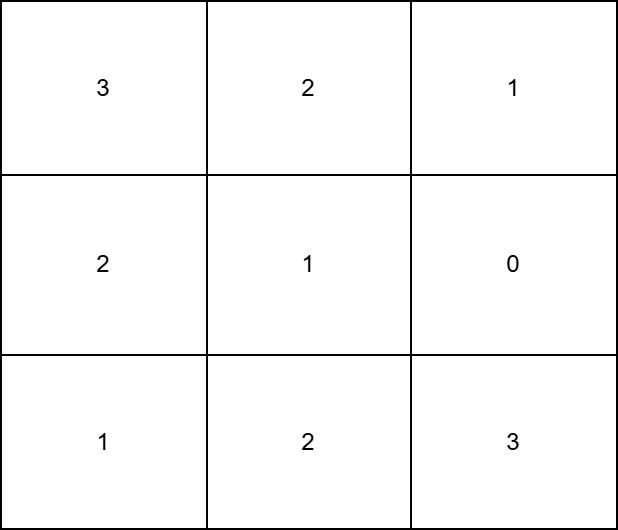
Input: grid = [[3,2,1],[2,1,0],[1,2,3]]
Output: 12
Explanation:
- To make the
0thcolumn strictly increasing, we can apply 2 operations ongrid[1][0], and 4 operations ongrid[2][0]. - To make the
1stcolumn strictly increasing, we can apply 2 operations ongrid[1][1], and 2 operations ongrid[2][1]. - To make the
2ndcolumn strictly increasing, we can apply 2 operations ongrid[1][2].
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 500 <= grid[i][j] < 2500
Solution
public class Solution {
public int minimumOperations(int[][] grid) {
int ans = 0;
for (int c = 0; c < grid[0].length; ++c) {
for (int r = 1; r < grid.length; ++r) {
if (grid[r][c] <= grid[r - 1][c]) {
ans += grid[r - 1][c] + 1 - grid[r][c];
grid[r][c] = grid[r - 1][c] + 1;
}
}
}
return ans;
}
}

