LeetCode-in-Java

3327. Check if DFS Strings Are Palindromes

Hard

You are given a tree rooted at node 0, consisting of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to node i.

Consider an empty string dfsStr, and define a recursive function dfs(int x) that takes a node x as a parameter and performs the following steps in order:

• Iterate over each child y of x in increasing order of their numbers, and call dfs(y).
• Add the character s[x] to the end of the string dfsStr.

Note that dfsStr is shared across all recursive calls of dfs.

You need to find a boolean array answer of size n, where for each index i from 0 to n - 1, you do the following:

• Empty the string dfsStr and call dfs(i).
• If the resulting string dfsStr is a palindrome, then set answer[i] to true. Otherwise, set answer[i] to false.

Return the array answer.

A palindrome is a string that reads the same forward and backward.

Example 1:

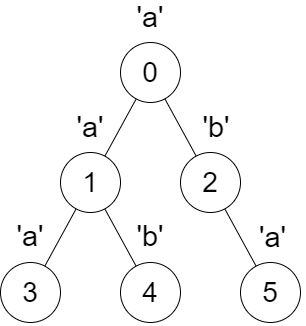
Input: parent = [-1,0,0,1,1,2], s = “aababa”

Output: [true,true,false,true,true,true]

Explanation:

• Calling dfs(0) results in the string dfsStr = "abaaba", which is a palindrome.
• Calling dfs(1) results in the string dfsStr = "aba", which is a palindrome.
• Calling dfs(2) results in the string dfsStr = "ab", which is not a palindrome.
• Calling dfs(3) results in the string dfsStr = "a", which is a palindrome.
• Calling dfs(4) results in the string dfsStr = "b", which is a palindrome.
• Calling dfs(5) results in the string dfsStr = "a", which is a palindrome.

Example 2:

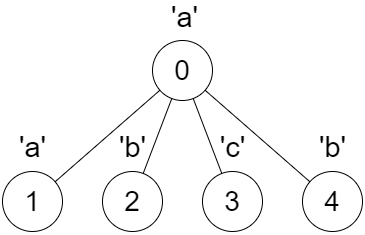
Input: parent = [-1,0,0,0,0], s = “aabcb”

Output: [true,true,true,true,true]

Explanation:

Every call on dfs(x) results in a palindrome string.

Constraints:

• n == parent.length == s.length
• 1 <= n <= 105
• 0 <= parent[i] <= n - 1 for all i >= 1.
• parent[0] == -1
• parent represents a valid tree.
• s consists only of lowercase English letters.

Solution

public class Solution {
    private int time = 0;
    private byte[] cs;
    private int[][] graph;

    public boolean[] findAnswer(int[] parent, String s) {
        int n = s.length();
        cs = s.getBytes();
        graph = new int[n][];
        final int[] childCount = new int[n];
        for (int i = 1; i < n; i++) {
            childCount[parent[i]]++;
        }
        for (int i = 0; i < n; i++) {
            graph[i] = new int[childCount[i]];
            childCount[i] = 0;
        }
        for (int i = 1; i < n; i++) {
            graph[parent[i]][childCount[parent[i]]++] = i;
        }
        byte[] dfsStr = new byte[n];
        int[] start = new int[n];
        int[] end = new int[n];
        dfs(0, dfsStr, start, end);
        int[] lens = getRadius(dfsStr);
        boolean[] ans = new boolean[n];
        for (int i = 0; i < n; i++) {
            int l = start[i];
            int r = end[i];
            int center = l + r + 2;
            ans[i] = lens[center] >= r - l + 1;
        }
        return ans;
    }

    private void dfs(int u, byte[] dfsStr, int[] start, int[] end) {
        start[u] = time;
        for (int v : graph[u]) {
            dfs(v, dfsStr, start, end);
        }
        dfsStr[time] = cs[u];
        end[u] = time++;
    }

    private int[] getRadius(byte[] cs) {
        int n = cs.length;
        byte[] t = new byte[2 * n + 3];
        int m = 0;
        t[m++] = '@';
        t[m++] = '#';
        for (byte c : cs) {
            t[m++] = c;
            t[m++] = '#';
        }
        t[m++] = '$';
        int[] lens = new int[m];
        int center = 0;
        int right = 0;
        for (int i = 2; i < m - 2; i++) {
            int len = 0;
            if (i < right) {
                len = Math.min(lens[2 * center - i], right - i);
            }
            while (t[i + len + 1] == t[i - len - 1]) {
                len++;
            }
            if (right < i + len) {
                right = i + len;
                center = i;
            }
            lens[i] = len;
        }
        return lens;
    }
}

This site is open source. Improve this page.