LeetCode-in-Java
3319. K-th Largest Perfect Subtree Size in Binary Tree
Medium
You are given the root of a binary tree and an integer k.
Return an integer denoting the size of the kth largest perfect binary subtree, or -1 if it doesn’t exist.
A perfect binary tree is a tree where all leaves are on the same level, and every parent has two children.
Example 1:
Input: root = [5,3,6,5,2,5,7,1,8,null,null,6,8], k = 2
Output: 3
Explanation:
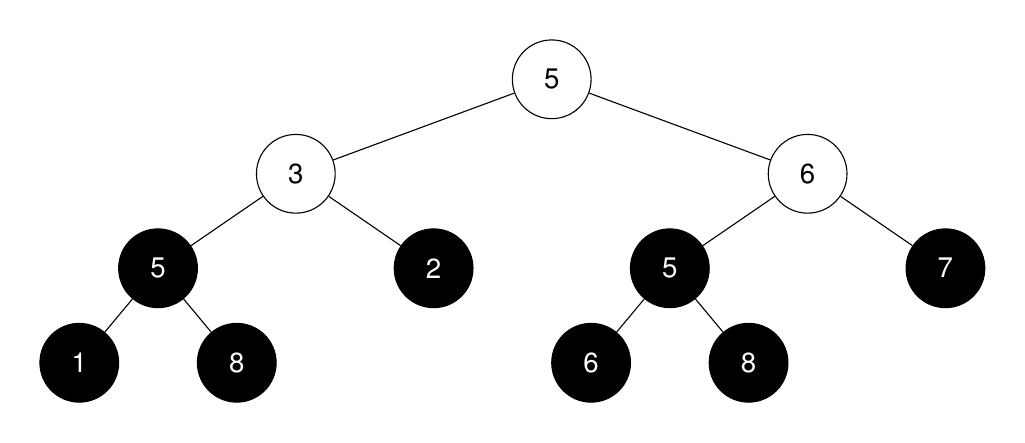
The roots of the perfect binary subtrees are highlighted in black. Their sizes, in non-increasing order are [3, 3, 1, 1, 1, 1, 1, 1].
The 2nd largest size is 3.
Example 2:
Input: root = [1,2,3,4,5,6,7], k = 1
Output: 7
Explanation:
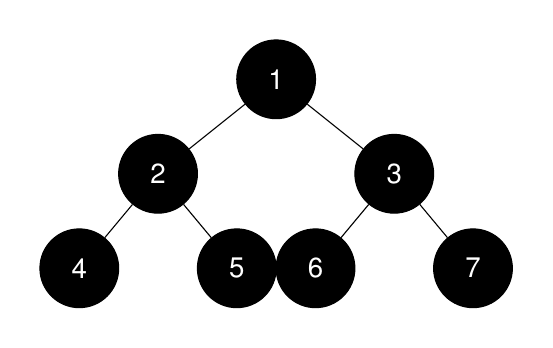
The sizes of the perfect binary subtrees in non-increasing order are [7, 3, 3, 1, 1, 1, 1]. The size of the largest perfect binary subtree is 7.
Example 3:
Input: root = [1,2,3,null,4], k = 3
Output: -1
Explanation:
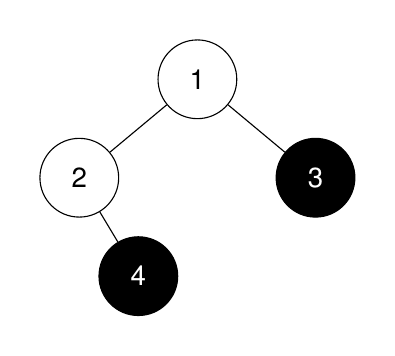
The sizes of the perfect binary subtrees in non-increasing order are [1, 1]. There are fewer than 3 perfect binary subtrees.
Constraints:
- The number of nodes in the tree is in the range
[1, 2000]. 1 <= Node.val <= 20001 <= k <= 1024
Solution
import com_github_leetcode.TreeNode;
import java.util.PriorityQueue;
import java.util.Queue;
/*
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
private final Queue<Integer> pq = new PriorityQueue<>();
public int kthLargestPerfectSubtree(TreeNode root, int k) {
dfs(root, k);
return pq.isEmpty() || pq.size() < k ? -1 : pq.peek();
}
private int dfs(TreeNode root, int k) {
if (root == null) {
return 0;
}
int left = dfs(root.left, k);
int right = dfs(root.right, k);
if (left == right) {
pq.offer(1 + left + right);
}
if (pq.size() > k) {
pq.poll();
}
return left == right ? 1 + left + right : -1;
}
}

