LeetCode-in-Java

3245. Alternating Groups III

Hard

There are some red and blue tiles arranged circularly. You are given an array of integers colors and a 2D integers array queries.

The color of tile i is represented by colors[i]:

• colors[i] == 0 means that tile i is red.
• colors[i] == 1 means that tile i is blue.

An alternating group is a contiguous subset of tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its adjacent tiles in the group).

You have to process queries of two types:

• queries[i] = [1, sizei], determine the count of alternating groups with size sizei.
• queries[i] = [2, indexi, colori], change colors[indexi] to colori.

Return an array answer containing the results of the queries of the first type in order.

Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.

Example 1:

Input: colors = [0,1,1,0,1], queries = [[2,1,0],[1,4]]

Output: [2]

Explanation:

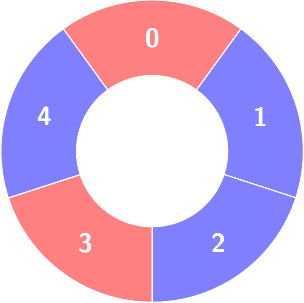
First query:

Change colors[1] to 0.

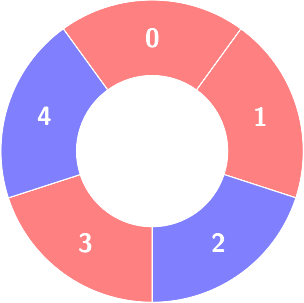
Second query:

Count of the alternating groups with size 4:

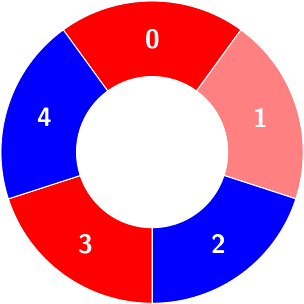
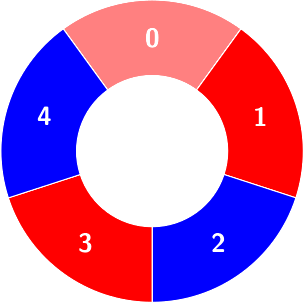
Example 2:

Input: colors = [0,0,1,0,1,1], queries = [[1,3],[2,3,0],[1,5]]

Output: [2,0]

Explanation:

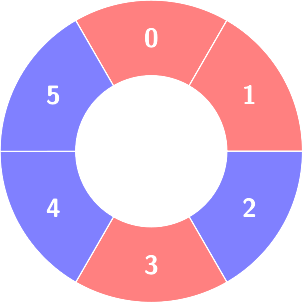
First query:

Count of the alternating groups with size 3:

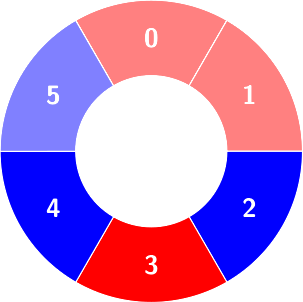
Second query: colors will not change.

Third query: There is no alternating group with size 5.

Constraints:

• 4 <= colors.length <= 5 * 104
• 0 <= colors[i] <= 1
• 1 <= queries.length <= 5 * 104
• queries[i][0] == 1 or queries[i][0] == 2
• For all i that:
  • queries[i][0] == 1: queries[i].length == 2, 3 <= queries[i][1] <= colors.length - 1
  • queries[i][0] == 2: queries[i].length == 3, 0 <= queries[i][1] <= colors.length - 1, 0 <= queries[i][2] <= 1

Solution

import java.util.ArrayList;
import java.util.BitSet;
import java.util.List;

public class Solution {
    public List<Integer> numberOfAlternatingGroups(int[] colors, int[][] queries) {
        int n = colors.length;
        BitSet set = new BitSet();
        BIT bit = new BIT(n);
        for (int i = 0; i < n; i++) {
            if (colors[i] == colors[getIndex(i + 1, n)]) {
                add(set, bit, n, i);
            }
        }
        List<Integer> ans = new ArrayList<>();
        for (int[] q : queries) {
            if (q[0] == 1) {
                if (set.isEmpty()) {
                    ans.add(n);
                } else {
                    int size = q[1];
                    int[] res = bit.query(size);
                    ans.add(res[1] - res[0] * (size - 1));
                }
            } else {
                int i = q[1];
                int color = colors[i];
                if (q[2] == color) {
                    continue;
                }
                int pre = getIndex(i - 1, n);
                if (colors[pre] == color) {
                    remove(set, bit, n, pre);
                }
                int next = getIndex(i + 1, n);
                if (colors[next] == color) {
                    remove(set, bit, n, i);
                }
                colors[i] ^= 1;
                color = colors[i];
                if (colors[pre] == color) {
                    add(set, bit, n, pre);
                }
                if (colors[next] == color) {
                    add(set, bit, n, i);
                }
            }
        }
        return ans;
    }

    private void add(BitSet set, BIT bit, int n, int i) {
        if (set.isEmpty()) {
            bit.update(n, 1);
        } else {
            update(set, bit, n, i, 1);
        }
        set.set(i);
    }

    private void remove(BitSet set, BIT bit, int n, int i) {
        set.clear(i);
        if (set.isEmpty()) {
            bit.update(n, -1);
        } else {
            update(set, bit, n, i, -1);
        }
    }

    private void update(BitSet set, BIT bit, int n, int i, int v) {
        int pre = set.previousSetBit(i);
        if (pre == -1) {
            pre = set.previousSetBit(n);
        }
        int next = set.nextSetBit(i);
        if (next == -1) {
            next = set.nextSetBit(0);
        }
        bit.update(getIndex(next - pre + n - 1, n) + 1, -v);
        bit.update(getIndex(i - pre, n), v);
        bit.update(getIndex(next - i, n), v);
    }

    private int getIndex(int index, int mod) {
        int result = index >= mod ? index - mod : index;
        return index < 0 ? index + mod : result;
    }

    private static class BIT {
        int n;
        int[] tree1;
        int[] tree2;

        BIT(int n) {
            this.n = n + 1;
            tree1 = new int[n + 1];
            tree2 = new int[n + 1];
        }

        void update(int size, int v) {
            for (int i = size; i > 0; i -= i & -i) {
                tree1[i] += v;
                tree2[i] += v * size;
            }
        }

        int[] query(int size) {
            int count = 0;
            int sum = 0;
            for (int i = size; i < n; i += i & -i) {
                count += tree1[i];
                sum += tree2[i];
            }
            return new int[] {count, sum};
        }
    }
}

This site is open source. Improve this page.