LeetCode-in-Java

3242. Design Neighbor Sum Service

Easy

You are given a n x n 2D array grid containing distinct elements in the range [0, n2 - 1].

Implement the neighborSum class:

• neighborSum(int [][]grid) initializes the object.
• int adjacentSum(int value) returns the sum of elements which are adjacent neighbors of value, that is either to the top, left, right, or bottom of value in grid.
• int diagonalSum(int value) returns the sum of elements which are diagonal neighbors of value, that is either to the top-left, top-right, bottom-left, or bottom-right of value in grid.

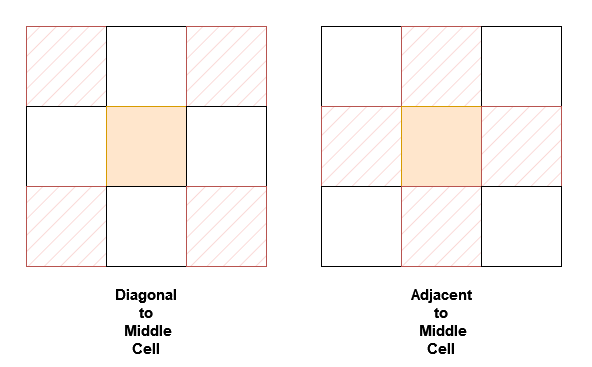
Example 1:

Input:

[“neighborSum”, “adjacentSum”, “adjacentSum”, “diagonalSum”, “diagonalSum”]

[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]

Output: [null, 6, 16, 16, 4]

Explanation:

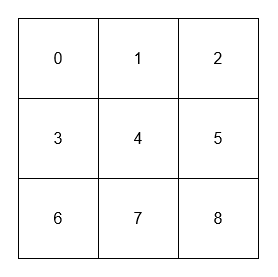
• The adjacent neighbors of 1 are 0, 2, and 4.
• The adjacent neighbors of 4 are 1, 3, 5, and 7.
• The diagonal neighbors of 4 are 0, 2, 6, and 8.
• The diagonal neighbor of 8 is 4.

Example 2:

Input:

[“neighborSum”, “adjacentSum”, “diagonalSum”]

[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]

Output: [null, 23, 45]

Explanation:

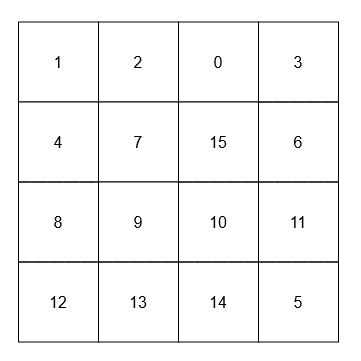
• The adjacent neighbors of 15 are 0, 10, 7, and 6.
• The diagonal neighbors of 9 are 4, 12, 14, and 15.

Constraints:

• 3 <= n == grid.length == grid[0].length <= 10
• 0 <= grid[i][j] <= n2 - 1
• All grid[i][j] are distinct.
• value in adjacentSum and diagonalSum will be in the range [0, n2 - 1].
• At most 2 * n2 calls will be made to adjacentSum and diagonalSum.

Solution

public class NeighborSum {
    private final int[][] grid;
    private final int n;
    private final int[] rowIndex;
    private final int[] colIndex;

    public NeighborSum(int[][] grid) {
        this.grid = grid;
        this.n = grid.length;
        this.rowIndex = new int[n * n];
        this.colIndex = new int[n * n];
        // Precompute the positions of each value in the grid for quick access
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                rowIndex[grid[i][j]] = i;
                colIndex[grid[i][j]] = j;
            }
        }
    }

    public int adjacentSum(int value) {
        int sum = 0;
        int i = rowIndex[value];
        int j = colIndex[value];
        // Check up
        if (i > 0) {
            sum += grid[i - 1][j];
        }
        // Check down
        if (i < n - 1) {
            sum += grid[i + 1][j];
        }
        // Check left
        if (j > 0) {
            sum += grid[i][j - 1];
        }
        // Check right
        if (j < n - 1) {
            sum += grid[i][j + 1];
        }
        return sum;
    }

    public int diagonalSum(int value) {
        int sum = 0;
        int i = rowIndex[value];
        int j = colIndex[value];
        // Check top-left
        if (i > 0 && j > 0) {
            sum += grid[i - 1][j - 1];
        }
        // Check top-right
        if (i > 0 && j < n - 1) {
            sum += grid[i - 1][j + 1];
        }
        // Check bottom-left
        if (i < n - 1 && j > 0) {
            sum += grid[i + 1][j - 1];
        }
        // Check bottom-right
        if (i < n - 1 && j < n - 1) {
            sum += grid[i + 1][j + 1];
        }
        return sum;
    }
}

/*
 * Your neighborSum object will be instantiated and called as such:
 * neighborSum obj = new neighborSum(grid);
 * int param_1 = obj.adjacentSum(value);
 * int param_2 = obj.diagonalSum(value);
 */

This site is open source. Improve this page.