LeetCode-in-Java

3197. Find the Minimum Area to Cover All Ones II

Hard

You are given a 2D binary array grid. You need to find 3 non-overlapping rectangles having non-zero areas with horizontal and vertical sides such that all the 1’s in grid lie inside these rectangles.

Return the minimum possible sum of the area of these rectangles.

Note that the rectangles are allowed to touch.

Example 1:

Input: grid = [[1,0,1],[1,1,1]]

Output: 5

Explanation:

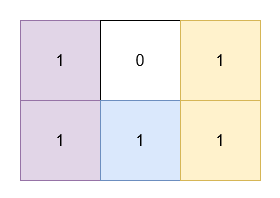
• The 1’s at (0, 0) and (1, 0) are covered by a rectangle of area 2.
• The 1’s at (0, 2) and (1, 2) are covered by a rectangle of area 2.
• The 1 at (1, 1) is covered by a rectangle of area 1.

Example 2:

Input: grid = [[1,0,1,0],[0,1,0,1]]

Output: 5

Explanation:

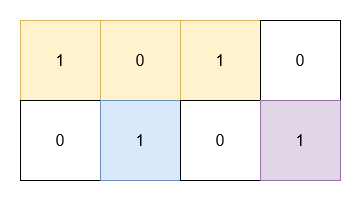
• The 1’s at (0, 0) and (0, 2) are covered by a rectangle of area 3.
• The 1 at (1, 1) is covered by a rectangle of area 1.
• The 1 at (1, 3) is covered by a rectangle of area 1.

Constraints:

• 1 <= grid.length, grid[i].length <= 30
• grid[i][j] is either 0 or 1.
• The input is generated such that there are at least three 1’s in grid.

Solution

@SuppressWarnings("java:S135")
public class Solution {
    // rectangle unit count
    private int[][] ruc;
    private int height;
    private int width;

    // r0, c0 incl., r1, c1 excl.
    private int unitsInRectangle(int r0, int c0, int r1, int c1) {
        return ruc[r1][c1] - ruc[r0][c1] - ruc[r1][c0] + ruc[r0][c0];
    }

    private int minArea(int r0, int c0, int r1, int c1) {
        if (unitsInRectangle(r0, c0, r1, c1) == 0) {
            return 0;
        }
        int minRow = r0;
        while (unitsInRectangle(r0, c0, minRow + 1, c1) == 0) {
            minRow++;
        }
        int maxRow = r1 - 1;
        while (unitsInRectangle(maxRow, c0, r1, c1) == 0) {
            maxRow--;
        }
        int minCol = c0;
        while (unitsInRectangle(r0, c0, r1, minCol + 1) == 0) {
            minCol++;
        }
        int maxCol = c1 - 1;
        while (unitsInRectangle(r0, maxCol, r1, c1) == 0) {
            maxCol--;
        }
        return (maxRow - minRow + 1) * (maxCol - minCol + 1);
    }

    private int minSum2(int r0, int c0, int r1, int c1, boolean splitVertical) {
        int min = Integer.MAX_VALUE;
        if (splitVertical) {
            for (int c = c0 + 1; c < c1; c++) {
                int a1 = minArea(r0, c0, r1, c);
                if (a1 == 0) {
                    continue;
                }
                int a2 = minArea(r0, c, r1, c1);
                if (a2 != 0) {
                    min = Math.min(min, a1 + a2);
                }
            }
        } else {
            for (int r = r0 + 1; r < r1; r++) {
                int a1 = minArea(r0, c0, r, c1);
                if (a1 == 0) {
                    continue;
                }
                int a2 = minArea(r, c0, r1, c1);
                if (a2 != 0) {
                    min = Math.min(min, a1 + a2);
                }
            }
        }
        return min;
    }

    private int minSum3(
            boolean firstSplitVertical, boolean takeLower, boolean secondSplitVertical) {
        int min = Integer.MAX_VALUE;
        if (firstSplitVertical) {
            for (int c = 1; c < width; c++) {
                int a1;
                int a2;
                if (takeLower) {
                    a1 = minArea(0, 0, height, c);
                    if (a1 == 0) {
                        continue;
                    }
                    a2 = minSum2(0, c, height, width, secondSplitVertical);
                } else {
                    a1 = minArea(0, c, height, width);
                    if (a1 == 0) {
                        continue;
                    }
                    a2 = minSum2(0, 0, height, c, secondSplitVertical);
                }
                if (a2 != Integer.MAX_VALUE) {
                    min = Math.min(min, a1 + a2);
                }
            }
        } else {
            for (int r = 1; r < height; r++) {
                int a1;
                int a2;
                if (takeLower) {
                    a1 = minArea(0, 0, r, width);
                    if (a1 == 0) {
                        continue;
                    }
                    a2 = minSum2(r, 0, height, width, secondSplitVertical);
                } else {
                    a1 = minArea(r, 0, height, width);
                    if (a1 == 0) {
                        continue;
                    }
                    a2 = minSum2(0, 0, r, width, secondSplitVertical);
                }
                if (a2 != Integer.MAX_VALUE) {
                    min = Math.min(min, a1 + a2);
                }
            }
        }
        return min;
    }

    public int minimumSum(int[][] grid) {
        height = grid.length;
        width = grid[0].length;
        ruc = new int[height + 1][width + 1];
        for (int i = 0; i < height; i++) {
            int[] gRow = grid[i];
            int[] cRow0 = ruc[i];
            int[] cRow1 = ruc[i + 1];
            int c = 0;
            for (int j = 0; j < width; j++) {
                c += gRow[j];
                cRow1[j + 1] = cRow0[j + 1] + c;
            }
        }
        int min = Integer.MAX_VALUE;
        min = Math.min(min, minSum3(true, true, true));
        min = Math.min(min, minSum3(true, true, false));
        min = Math.min(min, minSum3(true, false, false));
        min = Math.min(min, minSum3(false, true, true));
        min = Math.min(min, minSum3(false, true, false));
        min = Math.min(min, minSum3(false, false, true));
        return min;
    }
}

This site is open source. Improve this page.