LeetCode-in-Java

3148. Maximum Difference Score in a Grid

Medium

You are given an m x n matrix grid consisting of positive integers. You can move from a cell in the matrix to any other cell that is either to the bottom or to the right (not necessarily adjacent). The score of a move from a cell with the value c1 to a cell with the value c2 is c2 - c1.

You can start at any cell, and you have to make at least one move.

Return the maximum total score you can achieve.

Example 1:

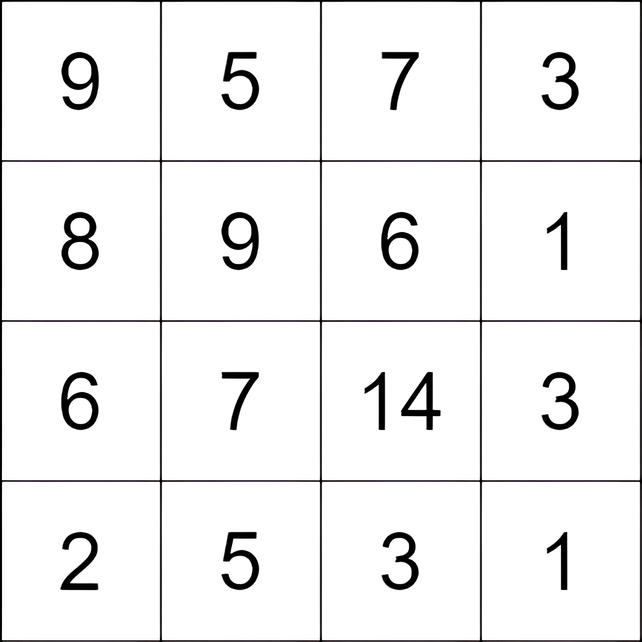
Input: grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

Output: 9

Explanation: We start at the cell (0, 1), and we perform the following moves:

• Move from the cell (0, 1) to (2, 1) with a score of 7 - 5 = 2.

• Move from the cell (2, 1) to (2, 2) with a score of 14 - 7 = 7.

The total score is 2 + 7 = 9.

Example 2:

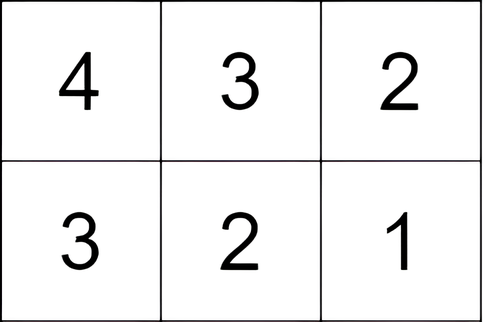
Input: grid = [[4,3,2],[3,2,1]]

Output: -1

Explanation: We start at the cell (0, 0), and we perform one move: (0, 0) to (0, 1). The score is 3 - 4 = -1.

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 105

Solution

import java.util.List;

public class Solution {
    public int maxScore(List<List<Integer>> grid) {
        int m = grid.size() - 1;
        List<Integer> row = grid.get(m);
        int n = row.size();
        int[] maxRB = new int[n--];
        int mx = maxRB[n] = row.get(n);
        int result = Integer.MIN_VALUE;
        for (int i = n - 1; i >= 0; i--) {
            int x = row.get(i);
            result = Math.max(result, mx - x);
            maxRB[i] = mx = Math.max(mx, x);
        }
        for (int i = m - 1; i >= 0; i--) {
            row = grid.get(i);
            mx = 0;
            for (int j = n; j >= 0; j--) {
                mx = Math.max(mx, maxRB[j]);
                int x = row.get(j);
                result = Math.max(result, mx - x);
                maxRB[j] = mx = Math.max(mx, x);
            }
        }
        return result;
    }
}

This site is open source. Improve this page.