LeetCode-in-Java

2924. Find Champion II

Medium

There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.

You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.

A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.

Team a will be the champion of the tournament if there is no team b that is stronger than team a.

Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.

Notes

• A cycle is a series of nodes a1, a2, ..., an, an+1 such that node a1 is the same node as node an+1, the nodes a1, a2, ..., an are distinct, and there is a directed edge from the node ai to node ai+1 for every i in the range [1, n].
• A DAG is a directed graph that does not have any cycle.

Example 1:

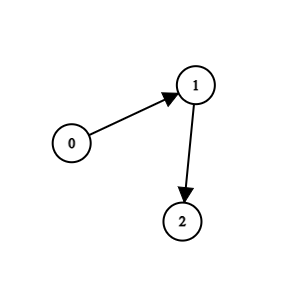
Input: n = 3, edges = [[0,1],[1,2]]

Output: 0

Explanation: Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.

Example 2:

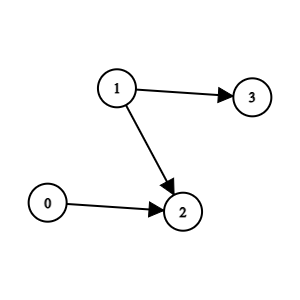
Input: n = 4, edges = [[0,2],[1,3],[1,2]]

Output: -1

Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.

Constraints:

• 1 <= n <= 100
• m == edges.length
• 0 <= m <= n * (n - 1) / 2
• edges[i].length == 2
• 0 <= edge[i][j] <= n - 1
• edges[i][0] != edges[i][1]
• The input is generated such that if team a is stronger than team b, team b is not stronger than team a.
• The input is generated such that if team a is stronger than team b and team b is stronger than team c, then team a is stronger than team c.

Solution

public class Solution {
    public int findChampion(int n, int[][] edges) {
        int[] arr = new int[n];
        for (int[] adj : edges) {
            arr[adj[1]]++;
        }
        int cnt = 0;
        int ans = -1;
        for (int i = 0; i < n; i++) {
            if (arr[i] == 0) {
                cnt++;
                ans = i;
            }
        }
        if (cnt == 1) {
            return ans;
        } else {
            return -1;
        }
    }
}

This site is open source. Improve this page.