LeetCode-in-Java

2920. Maximum Points After Collecting Coins From All Nodes

Hard

There exists an undirected tree rooted at node 0 with n nodes labeled from 0 to n - 1. You are given a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given a 0-indexed array coins of size n where coins[i] indicates the number of coins in the vertex i, and an integer k.

Starting from the root, you have to collect all the coins such that the coins at a node can only be collected if the coins of its ancestors have been already collected.

Coins at nodei can be collected in one of the following ways:

• Collect all the coins, but you will get coins[i] - k points. If coins[i] - k is negative then you will lose abs(coins[i] - k) points.
• Collect all the coins, but you will get floor(coins[i] / 2) points. If this way is used, then for all the nodej present in the subtree of nodei, coins[j] will get reduced to floor(coins[j] / 2).

Return the maximum points you can get after collecting the coins from all the tree nodes.

Example 1:

Input: edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5

Output: 11

Explanation:

Collect all the coins from node 0 using the first way. Total points = 10 - 5 = 5.

Collect all the coins from node 1 using the first way. Total points = 5 + (10 - 5) = 10.

Collect all the coins from node 2 using the second way so coins left at node 3 will be floor(3 / 2) = 1. Total points = 10 + floor(3 / 2) = 11.

Collect all the coins from node 3 using the second way. Total points = 11 + floor(1 / 2) = 11.

It can be shown that the maximum points we can get after collecting coins from all the nodes is 11.

Example 2:

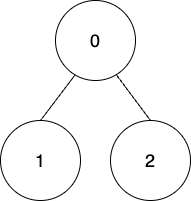
Input: edges = [[0,1],[0,2]], coins = [8,4,4], k = 0

Output: 16

Explanation: Coins will be collected from all the nodes using the first way. Therefore, total points = (8 - 0) + (4 - 0) + (4 - 0) = 16.

Constraints:

• n == coins.length
• 2 <= n <= 105
• 0 <= coins[i] <= 104
• edges.length == n - 1
• 0 <= edges[i][0], edges[i][1] < n
• 0 <= k <= 104

Solution

import java.util.ArrayList;
import java.util.List;

@SuppressWarnings("unchecked")
public class Solution {
    private List<Integer>[] adjList;
    private int[] coins;
    private int k;
    private int[][] dp;

    private void init(int[][] edges, int[] coins, int k) {
        int n = coins.length;
        adjList = new List[n];
        for (int v = 0; v < n; ++v) {
            adjList[v] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            adjList[u].add(v);
            adjList[v].add(u);
        }
        this.coins = coins;
        this.k = k;
        dp = new int[n][14];
        for (int v = 0; v < n; ++v) {
            for (int numOfWay2Parents = 0; numOfWay2Parents < 14; ++numOfWay2Parents) {
                dp[v][numOfWay2Parents] = -1;
            }
        }
    }

    private int rec(int v, int p, int numOfWay2Parents) {
        if (numOfWay2Parents >= 14) {
            return 0;
        }
        if (dp[v][numOfWay2Parents] == -1) {
            int coinsV = coins[v] / (1 << numOfWay2Parents);
            int s0 = coinsV - k;
            int s1 = coinsV / 2;
            for (int child : adjList[v]) {
                if (child != p) {
                    s0 += rec(child, v, numOfWay2Parents);
                    s1 += rec(child, v, numOfWay2Parents + 1);
                }
            }
            dp[v][numOfWay2Parents] = Math.max(s0, s1);
        }
        return dp[v][numOfWay2Parents];
    }

    public int maximumPoints(int[][] edges, int[] coins, int k) {
        init(edges, coins, k);
        return rec(0, -1, 0);
    }
}

This site is open source. Improve this page.