LeetCode-in-Java

2876. Count Visited Nodes in a Directed Graph

Hard

There is a directed graph consisting of n nodes numbered from 0 to n - 1 and n directed edges.

You are given a 0-indexed array edges where edges[i] indicates that there is an edge from node i to node edges[i].

Consider the following process on the graph:

• You start from a node x and keep visiting other nodes through edges until you reach a node that you have already visited before on this same process.

Return an array answer where answer[i] is the number of different nodes that you will visit if you perform the process starting from node i.

Example 1:

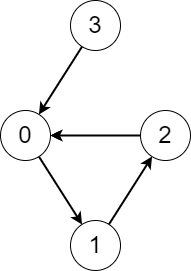
Input: edges = [1,2,0,0]

Output: [3,3,3,4]

Explanation: We perform the process starting from each node in the following way:

• Starting from node 0, we visit the nodes 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 3.
• Starting from node 1, we visit the nodes 1 -> 2 -> 0 -> 1. The number of different nodes we visit is 3.
• Starting from node 2, we visit the nodes 2 -> 0 -> 1 -> 2. The number of different nodes we visit is 3.
• Starting from node 3, we visit the nodes 3 -> 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 4.

Example 2:

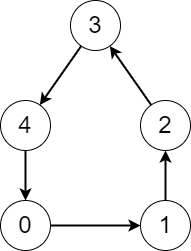
Input: edges = [1,2,3,4,0]

Output: [5,5,5,5,5]

Explanation: Starting from any node we can visit every node in the graph in the process.

Constraints:

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] <= n - 1
• edges[i] != i

Solution

import java.util.List;

public class Solution {
    public int[] countVisitedNodes(List<Integer> edges) {
        int n = edges.size();
        boolean[] visited = new boolean[n];
        int[] ans = new int[n];
        int[] level = new int[n];
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                visit(edges, 0, i, ans, visited, level);
            }
        }
        return ans;
    }

    private int[] visit(
            List<Integer> edges, int count, int curr, int[] ans, boolean[] visited, int[] level) {
        if (ans[curr] != 0) {
            return new int[] {-1, ans[curr]};
        }
        if (visited[curr]) {
            return new int[] {level[curr], count - level[curr]};
        }
        level[curr] = count;
        visited[curr] = true;
        int[] ret = visit(edges, count + 1, edges.get(curr), ans, visited, level);
        if (ret[0] == -1 || count < ret[0]) {
            ret[1]++;
        }
        ans[curr] = ret[1];
        return ret;
    }
}

This site is open source. Improve this page.