LeetCode-in-Java

2581. Count Number of Possible Root Nodes

Hard

Alice has an undirected tree with n nodes labeled from 0 to n - 1. The tree is represented as a 2D integer array edges of length n - 1 where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

Alice wants Bob to find the root of the tree. She allows Bob to make several guesses about her tree. In one guess, he does the following:

Chooses two distinct integers u and v such that there exists an edge [u, v] in the tree.
He tells Alice that u is the parent of v in the tree.

Bob’s guesses are represented by a 2D integer array guesses where guesses[j] = [u_j, v_j] indicates Bob guessed u_j to be the parent of v_j.

Alice being lazy, does not reply to each of Bob’s guesses, but just says that at least k of his guesses are true.

Given the 2D integer arrays edges, guesses and the integer k, return the number of possible nodes that can be the root of Alice’s tree. If there is no such tree, return 0.

Example 1:

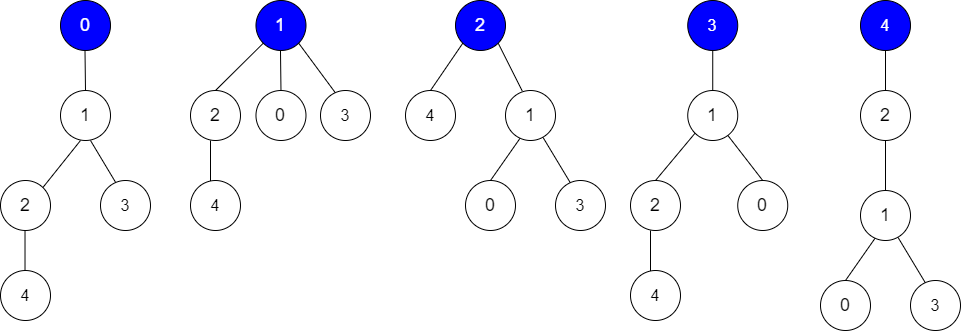
Input: edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3

Output: 3

Explanation:

Root = 0, correct guesses = [1,3], [0,1], [2,4]

Root = 1, correct guesses = [1,3], [1,0], [2,4]

Root = 2, correct guesses = [1,3], [1,0], [2,4]

Root = 3, correct guesses = [1,0], [2,4]

Root = 4, correct guesses = [1,3], [1,0]

Considering 0, 1, or 2 as root node leads to 3 correct guesses.

Example 2:

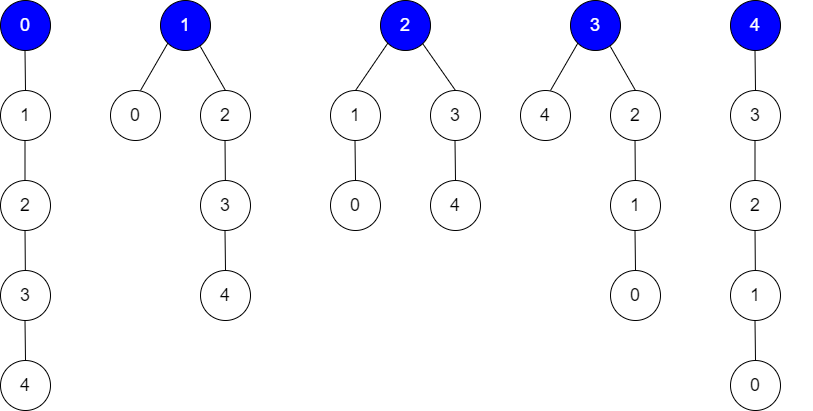
Input: edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1

Output: 5

Explanation:

Root = 0, correct guesses = [3,4]

Root = 1, correct guesses = [1,0], [3,4]

Root = 2, correct guesses = [1,0], [2,1], [3,4]

Root = 3, correct guesses = [1,0], [2,1], [3,2], [3,4]

Root = 4, correct guesses = [1,0], [2,1], [3,2]

Considering any node as root will give at least 1 correct guess.

Constraints:

edges.length == n - 1
2 <= n <= 10⁵
1 <= guesses.length <= 10⁵
0 <= a_i, b_i, u_j, v_j <= n - 1
a_i != b_i
u_j != v_j
edges represents a valid tree.
guesses[j] is an edge of the tree.
guesses is unique.
0 <= k <= guesses.length

Solution

import java.util.LinkedList;
import java.util.List;

@SuppressWarnings("unchecked")
public class Solution {
    public int rootCount(int[][] eg, int[][] gu, int k) {
        int n = eg.length + 1;
        List<Integer>[] g = new List[n];
        for (int i = 0; i < n; i++) {
            g[i] = new LinkedList<>();
        }
        for (int[] a : eg) {
            g[a[0]].add(a[1]);
            g[a[1]].add(a[0]);
        }
        int all = 0;
        int[] add = new int[n];
        int[] par = new int[n];
        dfs1(g, 0, -1, par);
        for (int[] a : gu) {
            if (par[a[1]] == a[0]) {
                all++;
                add[a[1]]--;
            } else {
                add[a[0]]++;
            }
        }
        dfs2(g, 0, -1, add);
        int ans = 0;
        for (int i : add) {
            if (i + all >= k) {
                ans++;
            }
        }
        return ans;
    }

    private void dfs1(List<Integer>[] g, int s, int p, int[] par) {
        par[s] = p;
        for (int i : g[s]) {
            if (i != p) {
                dfs1(g, i, s, par);
            }
        }
    }

    private void dfs2(List<Integer>[] g, int s, int p, int[] add) {
        for (int i : g[s]) {
            if (i != p) {
                add[i] += add[s];
                dfs2(g, i, s, add);
            }
        }
    }
}

This site is open source. Improve this page.