LeetCode-in-Java

2536. Increment Submatrices by One

Medium

You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.

You are also given a 2D integer array query. For each query[i] = [row1i, col1i, row2i, col2i], you should do the following operation:

• Add 1 to every element in the submatrix with the top left corner (row1i, col1i) and the bottom right corner (row2i, col2i). That is, add 1 to mat[x][y] for all row1i <= x <= row2i and col1i <= y <= col2i.

Return the matrix mat after performing every query.

Example 1:

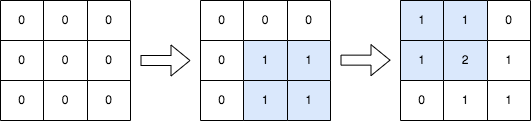
Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]

Output: [[1,1,0],[1,2,1],[0,1,1]]

Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.

• In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).

• In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).

Example 2:

Input: n = 2, queries = [[0,0,1,1]]

Output: [[1,1],[1,1]]

Explanation: The diagram above shows the initial matrix and the matrix after the first query.

• In the first query we add 1 to every element in the matrix.

Constraints:

• 1 <= n <= 500
• 1 <= queries.length <= 104
• 0 <= row1i <= row2i < n
• 0 <= col1i <= col2i < n

Solution

public class Solution {
    public int[][] rangeAddQueries(int n, int[][] queries) {
        int[][] g = new int[n][n];
        for (int[] q : queries) {
            int r1 = q[0];
            int c1 = q[1];
            int r2 = q[2];
            int c2 = q[3];
            g[r1][c1]++;
            if (c2 < n - 1) {
                g[r1][c2 + 1]--;
            }
            if (r2 < n - 1) {
                g[r2 + 1][c1]--;
            }
            if (c2 < n - 1 && r2 < n - 1) {
                g[r2 + 1][c2 + 1]++;
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (i > 0) {
                    g[i][j] += g[i - 1][j];
                }
                if (j > 0) {
                    g[i][j] += g[i][j - 1];
                }
                if (i > 0 && j > 0) {
                    g[i][j] -= g[i - 1][j - 1];
                }
            }
        }
        return g;
    }
}

This site is open source. Improve this page.