LeetCode-in-Java

2493. Divide Nodes Into the Maximum Number of Groups

Hard

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [a_i, b_i] indicates that there is a bidirectional edge between nodes a_i and b_i. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

Each node in the graph belongs to exactly one group.
For every pair of nodes in the graph that are connected by an edge [a_i, b_i], if a_i belongs to the group with index x, and b_i belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1:

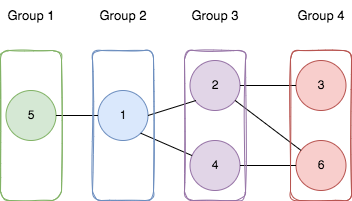
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]

Output: 4

Explanation: As shown in the image we:

Add node 5 to the first group.
Add node 1 to the second group.
Add nodes 2 and 4 to the third group.
Add nodes 3 and 6 to the fourth group.

We can see that every edge is satisfied. It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]

Output: -1

Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied. It can be shown that no grouping is possible.

Constraints:

1 <= n <= 500
1 <= edges.length <= 10⁴
edges[i].length == 2
1 <= a_i, b_i <= n
a_i != b_i
There is at most one edge between any pair of vertices.

Solution

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class Solution {
    public int magnificentSets(int n, int[][] edges) {
        List<List<Integer>> adj = new ArrayList<>();
        int[] visited = new int[n + 1];
        Arrays.fill(visited, -1);
        for (int i = 0; i <= n; i++) {
            adj.add(new ArrayList<>());
        }
        for (int[] edge : edges) {
            adj.get(edge[0]).add(edge[1]);
            adj.get(edge[1]).add(edge[0]);
        }
        int[] comp = new int[n + 1];
        int count = -1;
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            if (visited[i] == -1) {
                count++;
                comp[count] = bfs(i, adj, visited, count, n);
                if (comp[count] == -1) {
                    return -1;
                }
            } else {
                comp[visited[i]] = Math.max(comp[visited[i]], bfs(i, adj, visited, visited[i], n));
            }
        }
        for (int group : comp) {
            ans += group;
        }
        return ans;
    }

    private int bfs(int start, List<List<Integer>> adj, int[] visited, int count, int n) {
        Queue<Integer> q = new LinkedList<>();
        visited[start] = count;
        int ans = 1;
        int[] group = new int[n + 1];
        q.add(start);
        group[start] = 1;
        while (!q.isEmpty()) {
            int node = q.remove();
            for (int adjN : adj.get(node)) {
                if (group[adjN] == 0) {
                    visited[adjN] = count;
                    group[adjN] = group[node] + 1;
                    q.add(adjN);
                    ans = Math.max(ans, group[adjN]);
                } else if (Math.abs(group[adjN] - group[node]) != 1) {
                    return -1;
                }
            }
        }
        return ans;
    }
}

This site is open source. Improve this page.