LeetCode-in-Java

2373. Largest Local Values in a Matrix

Easy

You are given an n x n integer matrix grid.

Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:

• maxLocal[i][j] is equal to the largest value of the 3 x 3 matrix in grid centered around row i + 1 and column j + 1.

In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.

Return the generated matrix.

Example 1:

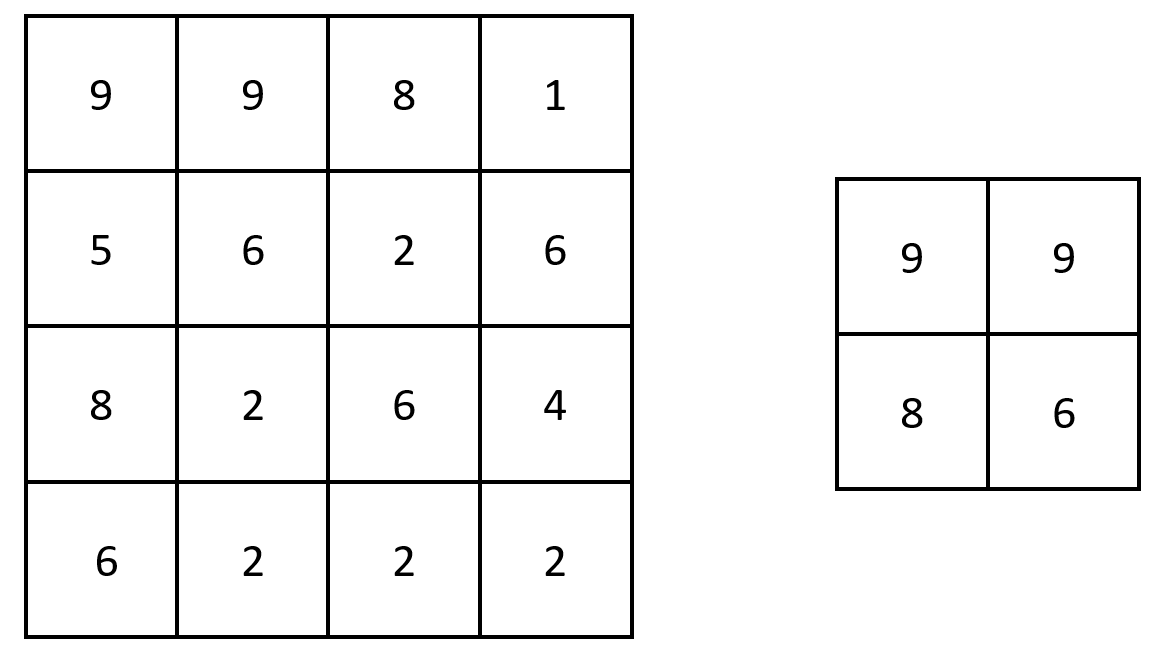
Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]

Output: [[9,9],[8,6]]

Explanation: The diagram above shows the original matrix and the generated matrix.

Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.

Example 2:

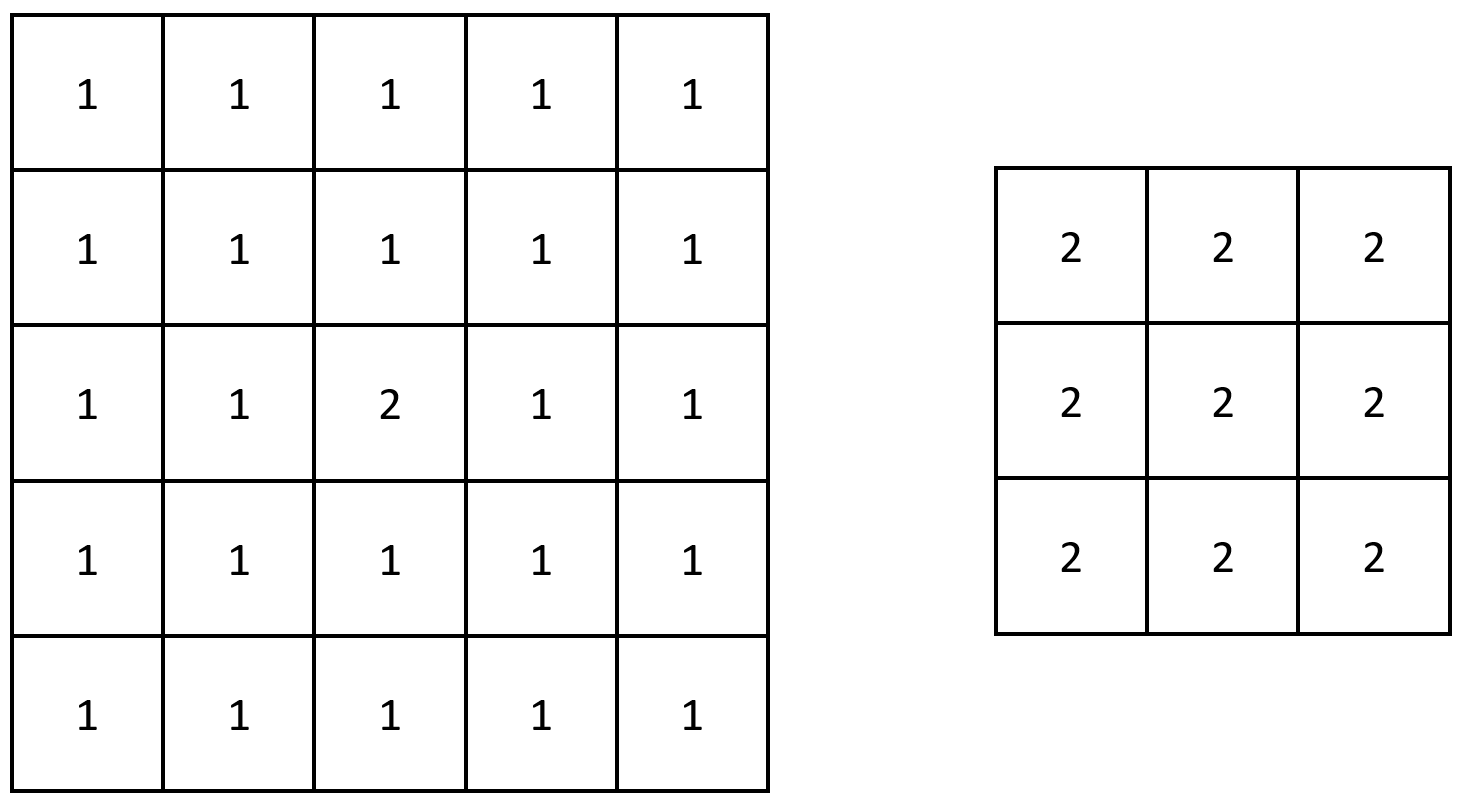
Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]

Output: [[2,2,2],[2,2,2],[2,2,2]]

Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.

Constraints:

• n == grid.length == grid[i].length
• 3 <= n <= 100
• 1 <= grid[i][j] <= 100

Solution

public class Solution {
    public int[][] largestLocal(int[][] grid) {
        int n = grid.length;
        int[][] res = new int[n - 2][n - 2];
        for (int i = 0; i < n - 2; i++) {
            for (int j = 0; j < n - 2; j++) {
                for (int p = i; p < i + 3; p++) {
                    for (int q = j; q < j + 3; q++) {
                        res[i][j] = Math.max(res[i][j], grid[p][q]);
                    }
                }
            }
        }
        return res;
    }
}

This site is open source. Improve this page.