LeetCode-in-Java
2328. Number of Increasing Paths in a Grid
Hard
You are given an m x n integer matrix grid, where you can move from a cell to any adjacent cell in all 4 directions.
Return the number of strictly increasing paths in the grid such that you can start from any cell and end at any cell. Since the answer may be very large, return it modulo 109 + 7.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
Example 1:
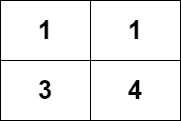
Input: grid = [[1,1],[3,4]]
Output: 8
Explanation: The strictly increasing paths are:
-
Paths with length 1: [1], [1], [3], [4].
-
Paths with length 2: [1 -> 3], [1 -> 4], [3 -> 4].
-
Paths with length 3: [1 -> 3 -> 4].
The total number of paths is 4 + 3 + 1 = 8.
Example 2:
Input: grid = [[1],[2]]
Output: 3
Explanation: The strictly increasing paths are:
-
Paths with length 1: [1], [2].
-
Paths with length 2: [1 -> 2].
The total number of paths is 2 + 1 = 3.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 1051 <= grid[i][j] <= 105
Solution
public class Solution {
private int help(int[][] a, int i, int j, int n, int m, int[][] dp) {
if (i < 0 || i >= n || j >= m || j < 0) {
return 0;
}
if (dp[i][j] != 0) {
return dp[i][j];
}
long res = 0;
if (i < n - 1 && a[i + 1][j] > a[i][j]) {
res += 1 + help(a, i + 1, j, n, m, dp);
}
if (i > 0 && a[i - 1][j] > a[i][j]) {
res += 1 + help(a, i - 1, j, n, m, dp);
}
if (j > 0 && a[i][j - 1] > a[i][j]) {
res += 1 + help(a, i, j - 1, n, m, dp);
}
if (j < m - 1 && a[i][j + 1] > a[i][j]) {
res += 1 + help(a, i, j + 1, n, m, dp);
}
dp[i][j] = (int) res % 1000000007;
return dp[i][j];
}
public int countPaths(int[][] grid) {
int n = grid.length;
int m = grid[0].length;
long ans = (long) n * m;
int[][] dp = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
ans += help(grid, i, j, n, m, dp) % 1000000007;
}
}
ans = ans % 1000000007;
return (int) ans;
}
}

