LeetCode-in-Java

2162. Minimum Cost to Set Cooking Time

Medium

A generic microwave supports cooking times for:

• at least 1 second.
• at most 99 minutes and 99 seconds.

To set the cooking time, you push at most four digits. The microwave normalizes what you push as four digits by prepending zeroes. It interprets the first two digits as the minutes and the last two digits as the seconds. It then adds them up as the cooking time. For example,

• You push 9 5 4 (three digits). It is normalized as 0954 and interpreted as 9 minutes and 54 seconds.
• You push 0 0 0 8 (four digits). It is interpreted as 0 minutes and 8 seconds.
• You push 8 0 9 0. It is interpreted as 80 minutes and 90 seconds.
• You push 8 1 3 0. It is interpreted as 81 minutes and 30 seconds.

You are given integers startAt, moveCost, pushCost, and targetSeconds. Initially, your finger is on the digit startAt. Moving the finger above any specific digit costs moveCost units of fatigue. Pushing the digit below the finger once costs pushCost units of fatigue.

There can be multiple ways to set the microwave to cook for targetSeconds seconds but you are interested in the way with the minimum cost.

Return the minimum cost to set targetSeconds seconds of cooking time.

Remember that one minute consists of 60 seconds.

Example 1:

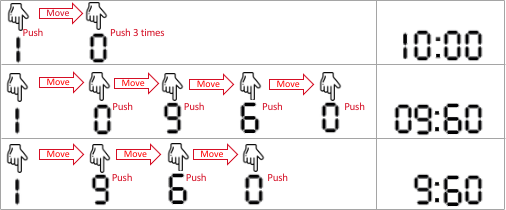
Input: startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600

Output: 6

Explanation: The following are the possible ways to set the cooking time.

• 1 0 0 0, interpreted as 10 minutes and 0 seconds.

The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).

The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.

• 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.

The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).

The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.

• 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.

The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).

The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.

Example 2:

Input: startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76

Output: 6

Explanation: The optimal way is to push two digits: 7 6, interpreted as 76 seconds.

The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2).

The total cost is: 1 + 2 + 1 + 2 = 6

Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.

Constraints:

• 0 <= startAt <= 9
• 1 <= moveCost, pushCost <= 105
• 1 <= targetSeconds <= 6039

Solution

public class Solution {
    public int minCostSetTime(int startAt, int moveCost, int pushCost, int targetSeconds) {
        int mins = targetSeconds / 60;
        int secs = targetSeconds % 60;
        return Math.min(
                cost(mins, secs, startAt, moveCost, pushCost),
                cost(mins - 1, secs + 60, startAt, moveCost, pushCost));
    }

    private int cost(int mins, int secs, int startAt, int moveCost, int pushCost) {
        if (mins > 99 || secs > 99 || mins < 0 || secs < 0) {
            return Integer.MAX_VALUE;
        }
        String s = Integer.toString(mins * 100 + secs);
        char curr = (char) (startAt + '0');
        int res = 0;
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == curr) {
                res += pushCost;
            } else {
                res += pushCost + moveCost;
                curr = s.charAt(i);
            }
        }
        return res;
    }
}

This site is open source. Improve this page.