LeetCode-in-Java
2054. Two Best Non-Overlapping Events
Medium
You are given a 0-indexed 2D integer array of events where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimei and ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.
Return this maximum sum.
Note that the start time and end time is inclusive: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.
Example 1:
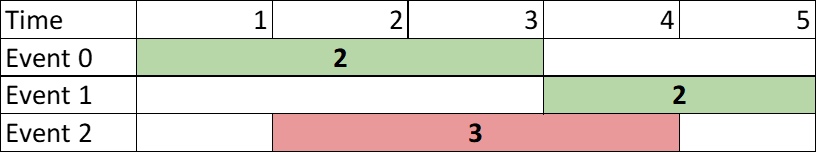
Input: events = [[1,3,2],[4,5,2],[2,4,3]]
Output: 4
Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.
Example 2:

Input: events = [[1,3,2],[4,5,2],[1,5,5]]
Output: 5
Explanation: Choose event 2 for a sum of 5.
Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]]
Output: 8
Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.
Constraints:
2 <= events.length <= 105events[i].length == 31 <= startTimei <= endTimei <= 1091 <= valuei <= 106
Solution
import java.util.Arrays;
public class Solution {
public int maxTwoEvents(int[][] events) {
Arrays.sort(events, (a, b) -> a[0] - b[0]);
int[] max = new int[events.length];
for (int i = events.length - 1; i >= 0; i--) {
if (i == events.length - 1) {
max[i] = events[i][2];
} else {
max[i] = Math.max(events[i][2], max[i + 1]);
}
}
int ans = 0;
for (int i = 0; i < events.length; i++) {
int end = events[i][1];
int left = i + 1;
int right = events.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (events[mid][0] <= end) {
left = mid + 1;
} else {
right = mid;
}
}
int value = events[i][2];
if (right >= 0 && right < events.length) {
value += max[right];
}
ans = Math.max(ans, value);
}
return ans;
}
}

