LeetCode-in-Java

1901. Find a Peak Element II

Medium

A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.

Given a 0-indexed m x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array [i,j].

You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.

You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.

Example 1:

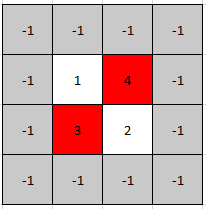
Input: mat = [[1,4],[3,2]]

Output: [0,1]

Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.

Example 2:

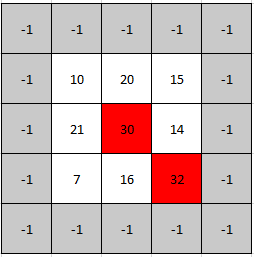
Input: mat = [[10,20,15],[21,30,14],[7,16,32]]

Output: [1,1]

Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 500
• 1 <= mat[i][j] <= 105
• No two adjacent cells are equal.

Solution

public class Solution {
    public int[] findPeakGrid(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        int l = 0;
        int r = m - 1;
        int mid;
        while (l <= r) {
            mid = (l + r) / 2;
            int mx = mat[0][mid];
            int mxi = 0;
            for (int i = 1; i < n; i++) {
                if (mx < mat[i][mid]) {
                    mx = mat[i][mid];
                    mxi = i;
                }
            }
            int lv = mid > l ? mat[mxi][mid - 1] : -1;
            int rv = mid < r ? mat[mxi][mid + 1] : -1;
            if (mx > lv && mx > rv) {
                return new int[] {mxi, mid};
            } else if (mx > lv) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return new int[] {-1, -1};
    }
}

This site is open source. Improve this page.