LeetCode-in-Java

1444. Number of Ways of Cutting a Pizza

Hard

Given a rectangular pizza represented as a rows x cols matrix containing the following characters: 'A' (an apple) and '.' (empty cell) and given the integer k. You have to cut the pizza into k pieces using k-1 cuts.

For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.

_Return the number of ways of cutting the pizza such that each piece contains at least one apple. _Since the answer can be a huge number, return this modulo 10^9 + 7.

Example 1:

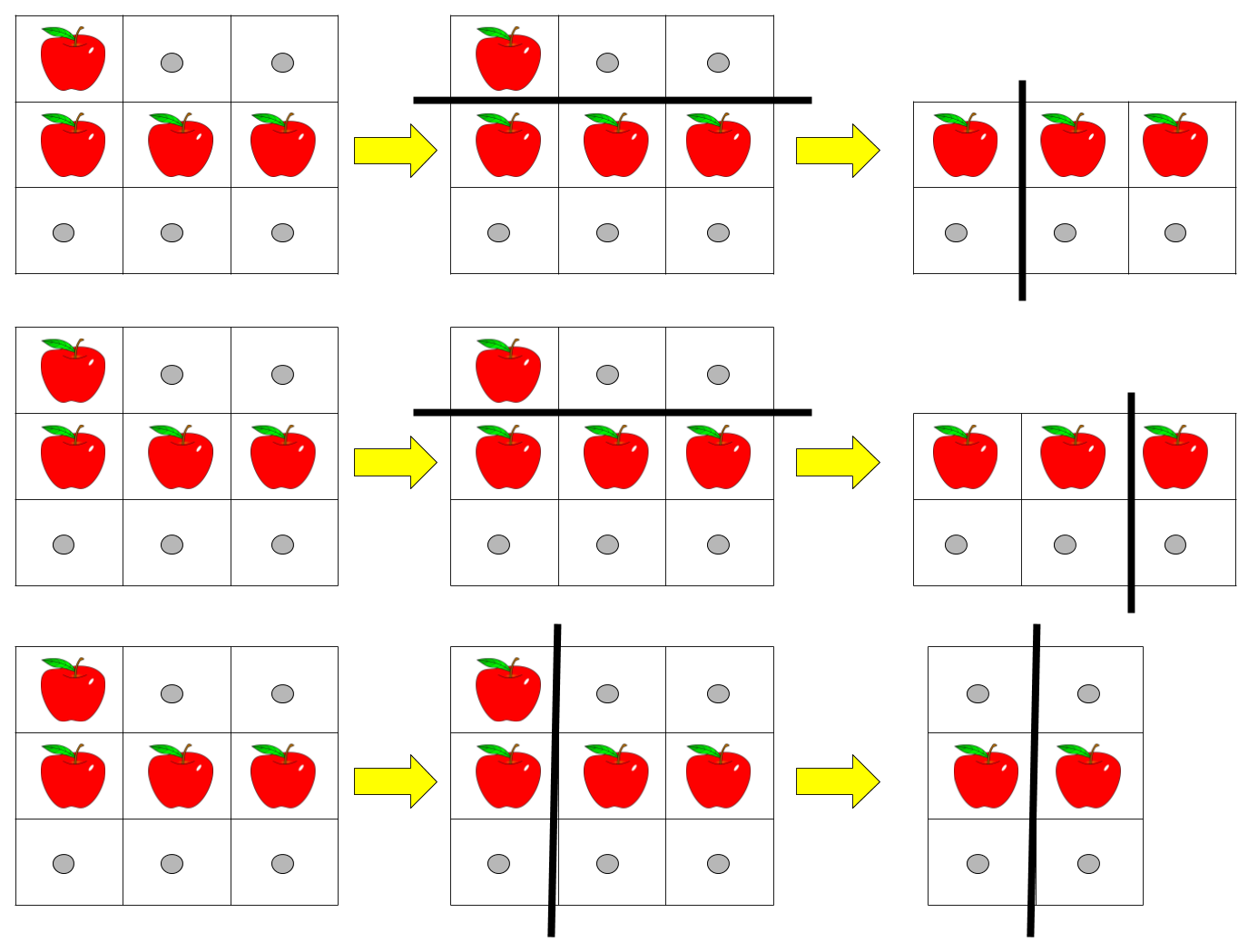
Input: pizza = [“A..”,”AAA”,”…”], k = 3

Output: 3

Explanation: The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.

Example 2:

Input: pizza = [“A..”,”AA.”,”…”], k = 3

Output: 1

Example 3:

Input: pizza = [“A..”,”A..”,”…”], k = 1

Output: 1

Constraints:

• 1 <= rows, cols <= 50
• rows == pizza.length
• cols == pizza[i].length
• 1 <= k <= 10
• pizza consists of characters 'A' and '.' only.

Solution

@SuppressWarnings("java:S2234")
public class Solution {
    private static final int K_MOD = (int) (1e9 + 7);

    public int ways(String[] pizza, int k) {
        if (pizza == null || pizza.length == 0) {
            return 0;
        }
        int m = pizza.length;
        int n = pizza[0].length();
        int[][] prefix = new int[m + 1][n + 1];

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                prefix[i + 1][j + 1] =
                        prefix[i][j + 1]
                                + prefix[i + 1][j]
                                + (pizza[i].charAt(j) == 'A' ? 1 : 0)
                                - prefix[i][j];
            }
        }
        int[][][] dp = new int[m][n][k];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                for (int s = 0; s < k; ++s) {
                    dp[i][j][s] = -1;
                }
            }
        }
        return dfs(0, 0, m, n, k - 1, prefix, dp);
    }

    private int dfs(int m, int n, int temp1, int temp2, int k, int[][] prefix, int[][][] dp) {
        if (k == 0) {
            return hasApple(prefix, m, n, temp1 - 1, temp2 - 1) ? 1 : 0;
        }
        if (dp[m][n][k] != -1) {
            return dp[m][n][k];
        }
        int local = 0;
        for (int x = m; x < temp1 - 1; ++x) {
            local =
                    (local
                                    + (hasApple(prefix, m, n, x, temp2 - 1) ? 1 : 0)
                                            * dfs(x + 1, n, temp1, temp2, k - 1, prefix, dp))
                            % K_MOD;
        }
        for (int y = n; y < temp2 - 1; ++y) {
            local =
                    (local
                                    + (hasApple(prefix, m, n, temp1 - 1, y) ? 1 : 0)
                                            * dfs(m, y + 1, temp1, temp2, k - 1, prefix, dp))
                            % K_MOD;
        }
        dp[m][n][k] = local;
        return dp[m][n][k];
    }

    private boolean hasApple(int[][] prefix, int x1, int y1, int x2, int y2) {
        return (prefix[x2 + 1][y2 + 1] - prefix[x1][y2 + 1] - prefix[x2 + 1][y1] + prefix[x1][y1])
                > 0;
    }
}

This site is open source. Improve this page.