LeetCode-in-Java
1361. Validate Binary Tree Nodes
Medium
You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.
If node i has no left child then leftChild[i] will equal -1, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
Example 1:
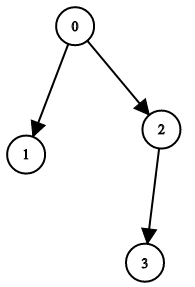
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true
Example 2:
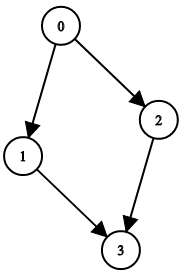
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false
Example 3:
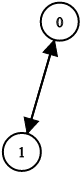
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false
Constraints:
n == leftChild.length == rightChild.length1 <= n <= 104-1 <= leftChild[i], rightChild[i] <= n - 1
Solution
import java.util.ArrayDeque;
import java.util.Deque;
public class Solution {
public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
int[] inDeg = new int[n];
for (int i = 0; i < n; i++) {
if (leftChild[i] >= 0) {
inDeg[leftChild[i]] += 1;
}
if (rightChild[i] >= 0) {
inDeg[rightChild[i]] += 1;
}
}
Deque<Integer> queue = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
if (inDeg[i] == 0) {
if (queue.isEmpty()) {
queue.offer(i);
} else {
// Violate rule 1.
return false;
}
}
if (inDeg[i] > 1) {
// Violate rule 2.
return false;
}
}
int tpLen = 0;
while (!queue.isEmpty()) {
int curNode = queue.poll();
tpLen++;
int left = leftChild[curNode];
int right = rightChild[curNode];
if (left > -1 && --inDeg[left] == 0) {
queue.offer(left);
}
if (right > -1 && --inDeg[right] == 0) {
queue.offer(right);
}
}
return tpLen == n;
}
}

