LeetCode-in-Java
1001. Grid Illumination
Hard
There is a 2D grid of size n x n where each cell of this grid has a lamp that is initially turned off.
You are given a 2D array of lamp positions lamps, where lamps[i] = [rowi, coli] indicates that the lamp at grid[rowi][coli] is turned on. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it illuminates its cell and all other cells in the same row, column, or diagonal.
You are also given another 2D array queries, where queries[j] = [rowj, colj]. For the jth query, determine whether grid[rowj][colj] is illuminated or not. After answering the jth query, turn off the lamp at grid[rowj][colj] and its 8 adjacent lamps if they exist. A lamp is adjacent if its cell shares either a side or corner with grid[rowj][colj].
Return an array of integers ans, where ans[j] should be 1 if the cell in the jth query was illuminated, or 0 if the lamp was not.
Example 1:
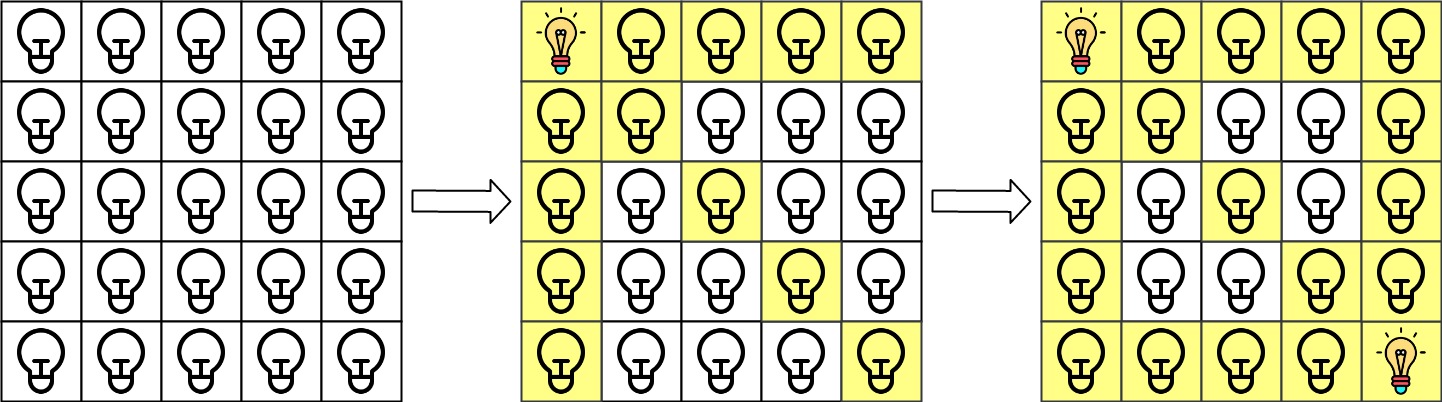
Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
Output: [1,0]
Explanation: We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid[0][0] then turning on the lamp at grid[4][4]. The 0th query asks if the lamp at grid[1][1] is illuminated or not (the blue square). It is illuminated, so set ans[0] = 1. Then, we turn off all lamps in the red square.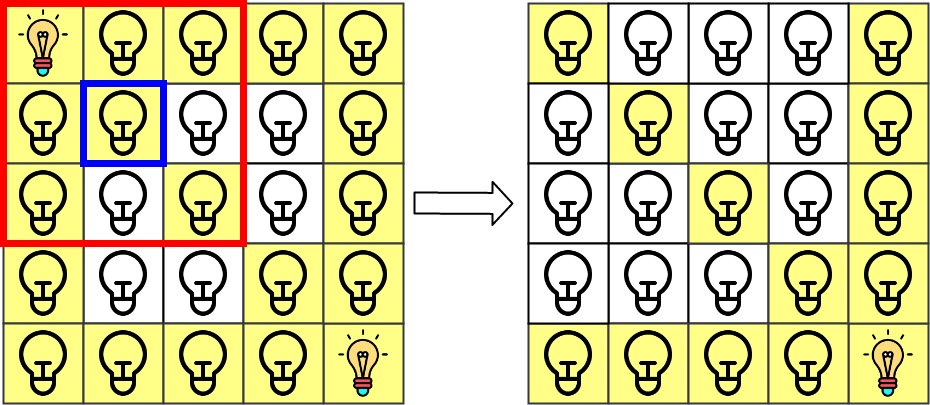 
The 1st query asks if the lamp at grid[1][0] is illuminated or not (the blue square). It is not illuminated, so set ans[1] = 0. Then, we turn off all lamps in the red rectangle.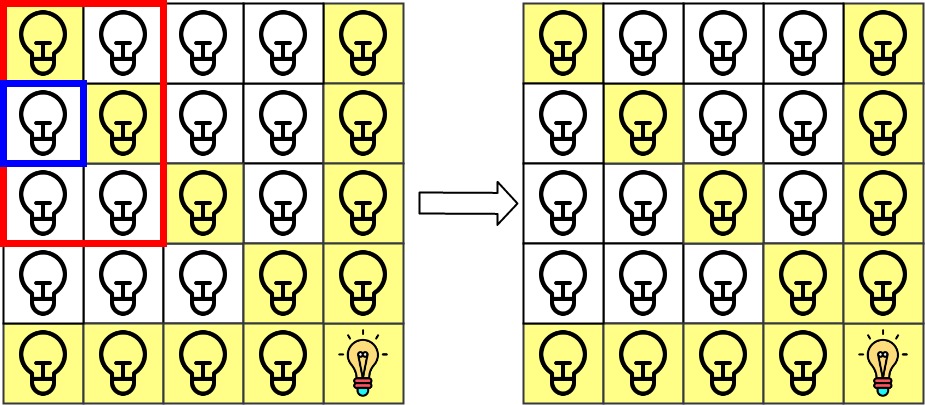 
Example 2:
Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
Output: [1,1]
Example 3:
Input: n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
Output: [1,1,0]
Constraints:
1 <= n <= 1090 <= lamps.length <= 200000 <= queries.length <= 20000lamps[i].length == 20 <= rowi, coli < nqueries[j].length == 20 <= rowj, colj < n
Solution
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;
public class Solution {
public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {
Map<Integer, Integer> rowIlluminations = new HashMap<>();
Map<Integer, Integer> colIlluminations = new HashMap<>();
Map<Integer, Integer> posDiagIlluminations = new HashMap<>();
Map<Integer, Integer> negDiagIlluminations = new HashMap<>();
Set<Long> lampPlacements = new HashSet<>();
for (int[] lamp : lamps) {
int row = lamp[0];
int col = lamp[1];
long key = row;
key = key * n + col;
if (lampPlacements.contains(key)) {
continue;
}
incr(rowIlluminations, row);
incr(colIlluminations, col);
incr(posDiagIlluminations, row + col);
incr(negDiagIlluminations, row + (n - 1 - col));
lampPlacements.add(key);
}
int[] ans = new int[queries.length];
for (int i = 0; i < ans.length; i++) {
int row = queries[i][0];
int col = queries[i][1];
if (rowIlluminations.containsKey(row)
|| colIlluminations.containsKey(col)
|| posDiagIlluminations.containsKey(row + col)
|| negDiagIlluminations.containsKey(row + (n - 1 - col))) {
ans[i] = 1;
}
int topRow = Math.max(0, row - 1);
int bottomRow = Math.min(n - 1, row + 1);
int leftCol = Math.max(0, col - 1);
int rightCol = Math.min(n - 1, col + 1);
for (int r = topRow; r <= bottomRow; r++) {
for (int c = leftCol; c <= rightCol; c++) {
long key = r;
key = key * n + c;
if (lampPlacements.contains(key)) {
decr(rowIlluminations, r);
decr(colIlluminations, c);
decr(posDiagIlluminations, r + c);
decr(negDiagIlluminations, r + (n - 1 - c));
lampPlacements.remove(key);
}
}
}
}
return ans;
}
private void incr(Map<Integer, Integer> map, int key) {
map.put(key, map.getOrDefault(key, 0) + 1);
}
private void decr(Map<Integer, Integer> map, int key) {
int v = map.get(key);
if (map.get(key) == 1) {
map.remove(key);
} else {
map.put(key, v - 1);
}
}
}