LeetCode-in-Java

787. Cheapest Flights Within K Stops

Medium

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

Example 1:

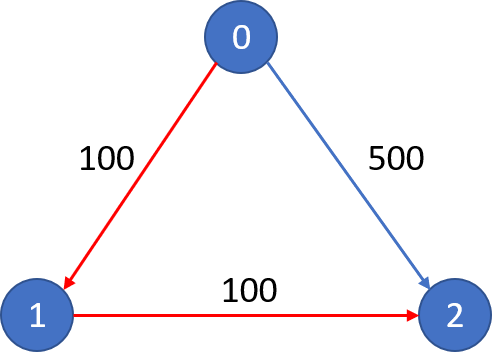
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1

Output: 200

Explanation:

The graph is shown.

The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2:

Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0

Output: 500

Explanation:

The graph is shown.

The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

Constraints:

• 1 <= n <= 100
• 0 <= flights.length <= (n * (n - 1) / 2)
• flights[i].length == 3
• 0 <= fromi, toi < n
• fromi != toi
• 1 <= pricei <= 104
• There will not be any multiple flights between two cities.
• 0 <= src, dst, k < n
• src != dst

Solution

import java.util.Arrays;

public class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        // k + 2 becase there are total of k(intermediate stops) + 1(src) + 1(dst)
        // dp[i][j] = cost to reach j using atmost i edges from src
        int[][] dp = new int[k + 2][n];
        for (int[] row : dp) {
            Arrays.fill(row, Integer.MAX_VALUE);
        }
        // cost to reach src is always 0
        for (int i = 0; i <= k + 1; i++) {
            dp[i][src] = 0;
        }
        // k+1 because k stops + dst
        for (int i = 1; i <= k + 1; i++) {
            for (int[] flight : flights) {
                int srcAirport = flight[0];
                int destAirport = flight[1];
                int cost = flight[2];
                // if cost to reach srcAirport in i - 1 steps is already found out then
                // the cost to reach destAirport will be min(cost to reach destAirport computed
                // already from some other srcAirport OR cost to reach srcAirport in i - 1 steps +
                // the cost to reach destAirport from srcAirport)
                if (dp[i - 1][srcAirport] != Integer.MAX_VALUE) {
                    dp[i][destAirport] = Math.min(dp[i][destAirport], dp[i - 1][srcAirport] + cost);
                }
            }
        }
        // checking for dp[k + 1][dst] because there are 'k + 2' airports in a path and distance
        // covered between 'k + 2' airports is 'k + 1'
        return dp[k + 1][dst] == Integer.MAX_VALUE ? -1 : dp[k + 1][dst];
    }
}

This site is open source. Improve this page.