LeetCode-in-Java

782. Transform to Chessboard

Hard

You are given an n x n binary grid board. In each move, you can swap any two rows with each other, or any two columns with each other.

Return the minimum number of moves to transform the board into a chessboard board. If the task is impossible, return -1.

A chessboard board is a board where no 0’s and no 1’s are 4-directionally adjacent.

Example 1:

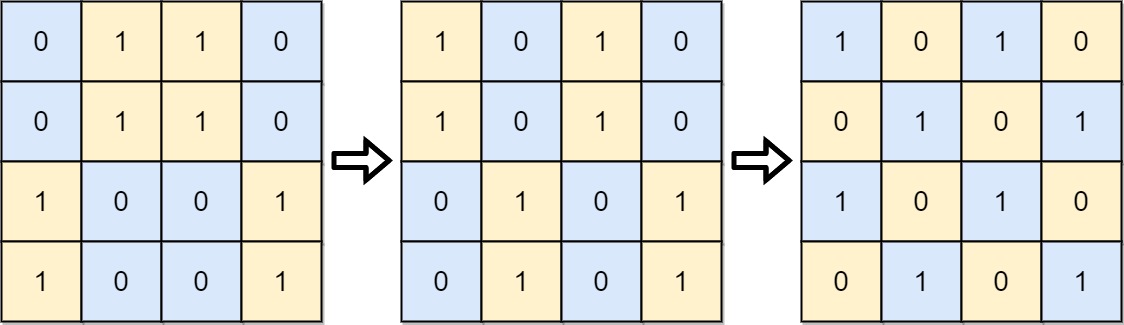
Input: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]

Output: 2

Explanation:

One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row. 

Example 2:

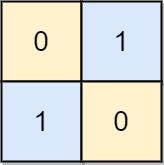
Input: board = [[0,1],[1,0]]

Output: 0

Explanation: Also note that the board with 0 in the top left corner, is also a valid chessboard.

Example 3:

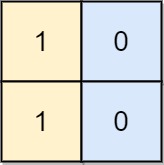
Input: board = [[1,0],[1,0]]

Output: -1

Explanation: No matter what sequence of moves you make, you cannot end with a valid chessboard.

Constraints:

• n == board.length
• n == board[i].length
• 2 <= n <= 30
• board[i][j] is either 0 or 1.

Solution

public class Solution {
    public int movesToChessboard(int[][] board) {
        int n = board.length;
        int colToMove = 0;
        int rowToMove = 0;
        int rowOneCnt = 0;
        int colOneCnt = 0;
        for (int[] ints : board) {
            for (int j = 0; j < n; j++) {
                if (((board[0][0] ^ ints[0]) ^ (ints[j] ^ board[0][j])) == 1) {
                    return -1;
                }
            }
        }
        for (int i = 0; i < n; i++) {
            rowOneCnt += board[0][i];
            colOneCnt += board[i][0];
            if (board[i][0] == i % 2) {
                rowToMove++;
            }
            if (board[0][i] == i % 2) {
                colToMove++;
            }
        }
        if (rowOneCnt < n / 2 || rowOneCnt > (n + 1) / 2) {
            return -1;
        }
        if (colOneCnt < n / 2 || colOneCnt > (n + 1) / 2) {
            return -1;
        }
        if (n % 2 == 1) {
            // we cannot make it when ..ToMove is odd
            if (colToMove % 2 == 1) {
                colToMove = n - colToMove;
            }
            if (rowToMove % 2 == 1) {
                rowToMove = n - rowToMove;
            }
        } else {
            colToMove = Math.min(colToMove, n - colToMove);
            rowToMove = Math.min(rowToMove, n - rowToMove);
        }
        return (colToMove + rowToMove) / 2;
    }
}

This site is open source. Improve this page.