LeetCode-in-Java

543. Diameter of Binary Tree

Easy

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1:

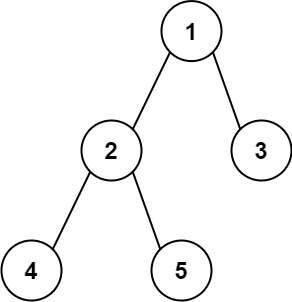
Input: root = [1,2,3,4,5]

Output: 3

Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]

Output: 1

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -100 <= Node.val <= 100

Solution

import com_github_leetcode.TreeNode;

/*
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int diameter;

    public int diameterOfBinaryTree(TreeNode root) {
        diameter = 0;
        diameterOfBinaryTreeUtil(root);
        return diameter;
    }

    private int diameterOfBinaryTreeUtil(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftLength = root.left != null ? 1 + diameterOfBinaryTreeUtil(root.left) : 0;
        int rightLength = root.right != null ? 1 + diameterOfBinaryTreeUtil(root.right) : 0;
        diameter = Math.max(diameter, leftLength + rightLength);
        return Math.max(leftLength, rightLength);
    }
}

Time Complexity (Big O Time):

The time complexity of the program is determined by the depth-first traversal of the binary tree. Specifically, the time complexity is governed by the diameterOfBinaryTreeUtil function, which recursively traverses the tree.

In each call to diameterOfBinaryTreeUtil, the program visits each node once. Therefore, the time complexity of visiting all nodes in the binary tree is O(n), where ‘n’ is the number of nodes in the tree.

Hence, the overall time complexity of the program is O(n), where ‘n’ is the number of nodes in the binary tree.

Space Complexity (Big O Space):

The space complexity of the program is determined by the function call stack during the recursive traversal of the binary tree.

1. The space used by the call stack is proportional to the height of the binary tree. In the worst case, when the tree is completely unbalanced (a skewed tree), the height of the tree can be ‘n’ (where ‘n’ is the number of nodes), resulting in a space complexity of O(n).

2. Additionally, the program uses a single integer variable diameter to keep track of the maximum diameter found during the traversal. This variable requires constant space, O(1).

Therefore, the overall space complexity of the program is O(n), where ‘n’ is the number of nodes in the binary tree. The dominant factor in the space complexity is the call stack space used during the recursion.

In summary, the provided program has a time complexity of O(n) and a space complexity of O(n), where ‘n’ is the number of nodes in the binary tree. It efficiently finds the diameter of the binary tree by performing a depth-first traversal.

This site is open source. Improve this page.