LeetCode-in-Java

240. Search a 2D Matrix II

Medium

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

Example 1:

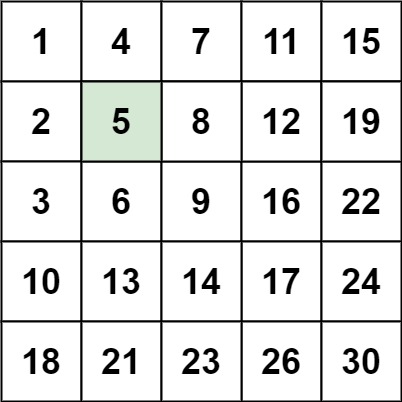
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5

Output: true

Example 2:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20

Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matrix[i][j] <= 109
• All the integers in each row are sorted in ascending order.
• All the integers in each column are sorted in ascending order.
• -109 <= target <= 109

Solution

public class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int r = 0;
        int c = matrix[0].length - 1;
        while (r < matrix.length && c >= 0) {
            if (matrix[r][c] == target) {
                return true;
            } else if (matrix[r][c] > target) {
                c--;
            } else {
                r++;
            }
        }
        return false;
    }
}

Time Complexity (Big O Time):

The time complexity of this program is primarily determined by the while loop. In the worst case, the while loop iterates until either r exceeds the number of rows (matrix.length) or c becomes negative. The loop condition ensures that we move either left (decreasing c) or down (increasing r) in each iteration. Since each iteration reduces the search space by one row or one column, the number of iterations in the worst case will be at most n + m, where n is the number of rows and m is the number of columns in the matrix.

Therefore, the time complexity of the program is O(n + m), where n is the number of rows and m is the number of columns in the matrix.

Space Complexity (Big O Space):

The program uses a few integer variables (r, c, target) that consume a constant amount of space regardless of the input size. These variables do not depend on the dimensions of the matrix.

Therefore, the space complexity of the program is O(1), which indicates constant space usage.

In summary, the provided program has a time complexity of O(n + m), where n is the number of rows and m is the number of columns in the matrix, and it has a space complexity of O(1), indicating constant space usage.

This site is open source. Improve this page.