LeetCode-in-Java

221. Maximal Square

Medium

Given an m x n binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.

Example 1:

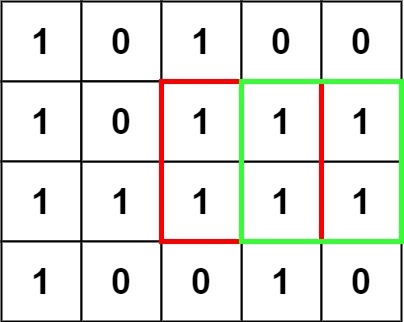
Input: matrix = [[“1”,”0”,”1”,”0”,”0”],[“1”,”0”,”1”,”1”,”1”],[“1”,”1”,”1”,”1”,”1”],[“1”,”0”,”0”,”1”,”0”]]

Output: 4

Example 2:

Input: matrix = [[“0”,”1”],[“1”,”0”]]

Output: 1

Example 3:

Input: matrix = [[“0”]]

Output: 0

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] is '0' or '1'.

Solution

public class Solution {
    public int maximalSquare(char[][] matrix) {
        int m = matrix.length;
        if (m == 0) {
            return 0;
        }
        int n = matrix[0].length;
        if (n == 0) {
            return 0;
        }
        int[][] dp = new int[m + 1][n + 1];
        int max = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    // 1 + minimum from cell above, cell to the left, cell diagonal upper-left
                    int next = 1 + Math.min(dp[i][j], Math.min(dp[i + 1][j], dp[i][j + 1]));
                    // keep track of the maximum value seen
                    if (next > max) {
                        max = next;
                    }
                    dp[i + 1][j + 1] = next;
                }
            }
        }
        return max * max;
    }
}

Time Complexity (Big O Time):

1. Initialization:
   • Initializing the m and n variables based on the dimensions of the input matrix takes O(1) time.
2. Dynamic Programming (DP) Table Initialization:
   • Creating a 2D DP table dp of size (m + 1) x (n + 1) takes O(m * n) time, where “m” and “n” are the dimensions of the input matrix.
3. DP Table Filling:
   • The program uses nested loops to iterate through each cell of the input matrix.
   • For each ‘1’ encountered in the input matrix, it updates the corresponding cell in the DP table based on the minimum value of its neighboring cells (above, left, and diagonal upper-left).
   • The nested loops iterate through all cells in the matrix once, and the updates for each cell take constant time.
   • Therefore, the time complexity for DP table filling is O(m * n).
4. Maximum Value Search:
   • During DP table filling, the program keeps track of the maximum value seen (max) in the DP table.
   • This also takes O(m * n) time since it iterates through all cells once.

Overall, the dominant factor in terms of time complexity is the DP table filling step, which is O(m * n).

Space Complexity (Big O Space):

1. DP Table (dp):
   • The space complexity of the DP table is O((m + 1) * (n + 1)), which simplifies to O(m * n) since the additional row and column are added for convenience.
   • Therefore, the space complexity is O(m * n) for the DP table.
2. Other Variables:
   • The space complexity for other variables like m, n, and max is O(1), as they occupy constant space.

In summary, the space complexity is primarily determined by the DP table, which is O(m * n), and the time complexity is dominated by the DP table filling step, also O(m * n).

This site is open source. Improve this page.