LeetCode-in-Java

148. Sort List

Medium

Given the head of a linked list, return the list after sorting it in ascending order.

Example 1:

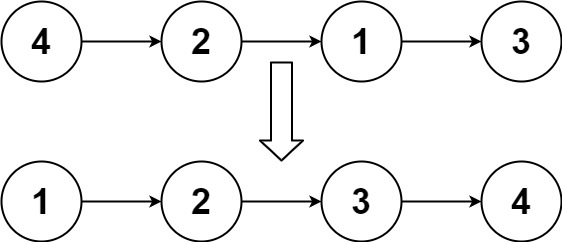
Input: head = [4,2,1,3]

Output: [1,2,3,4]

Example 2:

Input: head = [-1,5,3,4,0]

Output: [-1,0,3,4,5]

Example 3:

Input: head = []

Output: []

Constraints:

• The number of nodes in the list is in the range [0, 5 * 104].
• -105 <= Node.val <= 105

Follow up: Can you sort the linked list in O(n logn) time and O(1) memory (i.e. constant space)?

Solution

import com_github_leetcode.ListNode;

/*
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
@SuppressWarnings("java:S135")
public class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode slow = head;
        ListNode fast = head;
        ListNode pre = slow;
        while (fast != null && fast.next != null) {
            pre = slow;
            slow = slow.next;
            fast = fast.next.next;
        }
        pre.next = null;
        ListNode first = sortList(head);
        ListNode second = sortList(slow);
        ListNode res = new ListNode(1);
        ListNode cur = res;
        while (first != null || second != null) {
            if (first == null) {
                cur.next = second;
                break;
            } else if (second == null) {
                cur.next = first;
                break;
            } else if (first.val <= second.val) {
                cur.next = first;
                first = first.next;
                cur = cur.next;
            } else {
                cur.next = second;
                second = second.next;
                cur = cur.next;
            }
        }
        return res.next;
    }
}

Time Complexity (Big O Time):

The time complexity of the sortList method in this program is O(N*log(N)), where N is the number of nodes in the linked list. Here’s the breakdown:

• The recursive sortList function divides the linked list into two halves. This division step is performed in O(N/2) time, and it happens recursively, so it results in O(N*log(N)) time complexity.
• The merging step, where the two sorted halves are merged together, takes O(N) time in each recursive call.

Therefore, the overall time complexity of the sortList method is O(N*log(N)).

Space Complexity (Big O Space):

The space complexity of the sortList method is O(log(N)) on average due to the recursive function calls. This is because the space required for the function call stack during the recursion grows logarithmically with the number of elements in the list. Each recursive call creates a new stack frame with its own local variables.

Additionally, the program uses a few extra variables for pointers and a dummy node (res). These variables consume a constant amount of space, so they don’t significantly affect the overall space complexity.

In summary, the primary space consumption is due to the recursion stack, resulting in an average space complexity of O(log(N)) for this program.

This site is open source. Improve this page.