LeetCode-in-Java

104. Maximum Depth of Binary Tree

Easy

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

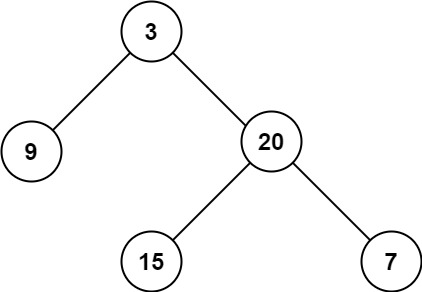
Input: root = [3,9,20,null,null,15,7]

Output: 3

Example 2:

Input: root = [1,null,2]

Output: 2

Example 3:

Input: root = []

Output: 0

Example 4:

Input: root = [0]

Output: 1

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -100 <= Node.val <= 100

To solve the “Maximum Depth of Binary Tree” problem in Java with a Solution class, we’ll perform a depth-first search (DFS) traversal of the binary tree. Below are the steps:

1. Create a Solution class: Define a class named Solution to encapsulate our solution methods.

2. Create a maxDepth method: This method takes the root node of the binary tree as input and returns its maximum depth.

3. Check for null root: Check if the root is null. If it is, return 0 as the depth.

4. Perform DFS traversal: Recursively compute the depth of the left and right subtrees. The maximum depth of the binary tree is the maximum depth of its left and right subtrees, plus 1 for the current node.

5. Return the result: After the DFS traversal is complete, return the maximum depth of the binary tree.

Here’s the Java implementation:

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0; // Check for empty tree
        int leftDepth = maxDepth(root.left); // Compute depth of left subtree
        int rightDepth = maxDepth(root.right); // Compute depth of right subtree
        return Math.max(leftDepth, rightDepth) + 1; // Return maximum depth of left and right subtrees, plus 1 for the current node
    }
    
    // Definition for a TreeNode
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        
        TreeNode() {}
        TreeNode(int val) { this.val = val; }
        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }
}

This implementation follows the steps outlined above and efficiently computes the maximum depth of the binary tree in Java using DFS traversal.

This site is open source. Improve this page.