LeetCode-in-Java

74. Search a 2D Matrix

Medium

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3

Output: true

Example 2:

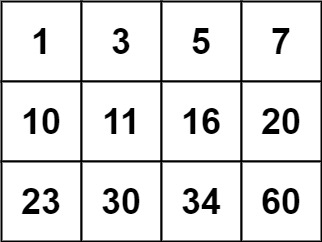
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13

Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

To solve the “Search a 2D Matrix” problem in Java with the Solution class, follow these steps:

1. Define a method searchMatrix in the Solution class that takes a 2D integer matrix matrix and an integer target as input and returns true if the target value is found in the matrix, otherwise returns false.
2. Initialize two pointers row and col to start at the top-right corner of the matrix. row starts from 0 and col starts from the last column.
3. Loop until row is less than the number of rows in the matrix and col is greater than or equal to 0:
   • If matrix[row][col] is equal to the target, return true.
   • If matrix[row][col] is greater than the target, decrement col.
   • If matrix[row][col] is less than the target, increment row.
4. If the target is not found after the loop, return false.

Here’s the implementation of the searchMatrix method in Java:

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        
        int row = 0;
        int col = n - 1;
        
        while (row < m && col >= 0) {
            if (matrix[row][col] == target) {
                return true;
            } else if (matrix[row][col] > target) {
                col--;
            } else {
                row++;
            }
        }
        
        return false;
    }
}

This implementation searches for the target value efficiently in the given matrix by starting from the top-right corner and moving either left or down based on the comparison with the target value. The time complexity of this solution is O(m + n), where m is the number of rows and n is the number of columns in the matrix.

This site is open source. Improve this page.